## Uncomment the following lines to set up the python environment
## Probably not needed depending on where you are running this notebook
#!pip install torch
#!pip install nilearn
#!pip install nibabel
#!pip install pandas
#!pip install sklearn
#!pip install matplotlib
#!pip install numpy
#!pip install torch torchvision
!git clone https://gitlab.inria.fr/epione_ML/mcvae.git
import sys
import os
sys.path.append(os.getcwd() + '/mcvae/src/')
import mcvae
print('Mcvae version:' + mcvae.__version__)
fatal: destination path 'mcvae' already exists and is not an empty directory.
Mcvae version:2.0.0
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.cross_decomposition import PLSCanonical, CCA
Random data generation¶
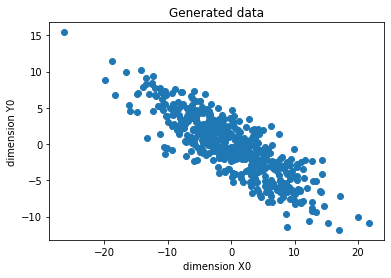
Our journey in the analysis of heterogeneous data starts with the generation of synthetic data. We first need to generate multivarite correlated random variables X and Y. To do so, we rely on the generative model we have seen during lesson:
# #############################################################################
# N subjects
n = 500
# here we define 2 Gaussian latents variables z = (l_1, l_2)
np.random.seed(42)
l1 = np.random.normal(size=n)
l2 = np.random.normal(size=n)
latents = np.array([l1, l2]).T
# We define two random transformations from the latent space to the space of X and Y respectively
transform_x = np.random.randint(-8,8, size = 10).reshape([2,5])
transform_y = np.random.randint(-8,8, size = 10).reshape([2,5])
# We compute data X = z w_x, and Y = z w_y
X = latents.dot(transform_x)
Y = latents.dot(transform_y)
# We add some random Gaussian noise
X = X + 2*np.random.normal(size = n*5).reshape((n, 5))
Y = Y + 2*np.random.normal(size = n*5).reshape((n, 5))
print('The latent space has dimension ' + str(latents.shape))
print('The transformation for X has dimension ' + str(transform_x.shape))
print('The transformation for Y has dimension ' + str(transform_y.shape))
print('X has dimension ' + str(X.shape))
print('Y has dimension ' + str(Y.shape))
The latent space has dimension (500, 2)
The transformation for X has dimension (2, 5)
The transformation for Y has dimension (2, 5)
X has dimension (500, 5)
Y has dimension (500, 5)
dimension_to_plot = 0
plt.scatter(X[:,1], Y[:,2])
plt.xlabel('dimension X' + str(dimension_to_plot))
plt.ylabel('dimension Y' + str(dimension_to_plot))
plt.title('Generated data')
plt.plot()
[]
PLS and scikit-learn: basic use¶
Our newly generated data can be already used to test the PLS and CCA provided by standard machie learning packages, such as scikit-learn.
##########################################################
# We first split the data in trainig and validation sets
# The training set is composed by a random sample of dimension N/2
train_idx = np.random.choice(range(X.shape[0]), size = int(X.shape[0]/2), replace = False)
X_train = X[train_idx, :]
# The testing set is composed by the remaining subjects
test_idx = np.where(np.in1d(range(X.shape[0]), train_idx, assume_unique =True, invert = True))[0]
X_test = X[test_idx, :]
# We reuse the same indices to split the data Y
Y_train = Y[train_idx, :]
Y_test = Y[test_idx, :]
#######################################
# We fit PLS as provided by scikit-learn
#Defining PLS object
plsca = PLSCanonical(n_components=2)
#Fitting on train data
plsca.fit(X_train, Y_train)
#We project the training data in the latent dimension
X_train_r, Y_train_r = plsca.transform(X_train, Y_train)
#We project the testing data in the latent dimension
X_test_r, Y_test_r = plsca.transform(X_test, Y_test)
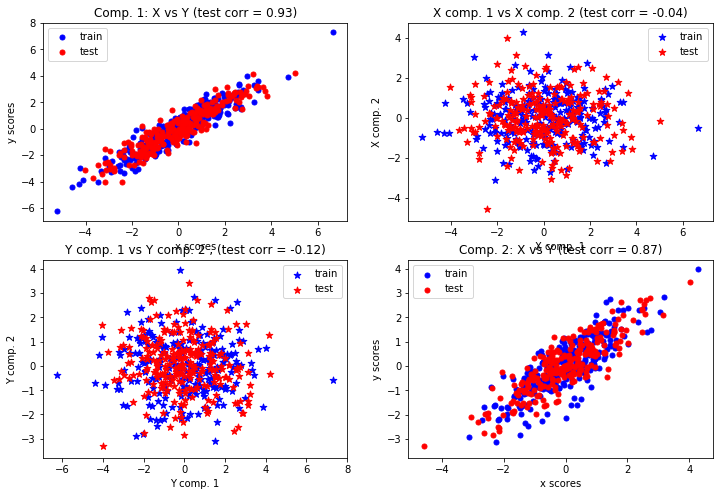
We note that the projections in the latent space retrieved by PLS are indeed correlated. The different dimensions of the projections are however uncorrelated.
# Scatter plot of scores
# ~~~~~~~~~~~~~~~~~~~~~~
# 1) On diagonal plot X vs Y scores on each components
plt.figure(figsize=(12, 8))
plt.subplot(221)
plt.scatter(X_train_r[:, 0], Y_train_r[:, 0], label="train",
marker="o", c="b", s=25)
plt.scatter(X_test_r[:, 0], Y_test_r[:, 0], label="test",
marker="o", c="r", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title('Comp. 1: X vs Y (test corr = %.2f)' %
np.corrcoef(X_test_r[:, 0], Y_test_r[:, 0])[0, 1])
plt.legend(loc="best")
plt.subplot(224)
plt.scatter(X_train_r[:, 1], Y_train_r[:, 1], label="train",
marker="o", c="b", s=25)
plt.scatter(X_test_r[:, 1], Y_test_r[:, 1], label="test",
marker="o", c="r", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title('Comp. 2: X vs Y (test corr = %.2f)' %
np.corrcoef(X_test_r[:, 1], Y_test_r[:, 1])[0, 1])
plt.legend(loc="best")
# 2) Off diagonal plot components 1 vs 2 for X and Y
plt.subplot(222)
plt.scatter(X_train_r[:, 0], X_train_r[:, 1], label="train",
marker="*", c="b", s=50)
plt.scatter(X_test_r[:, 0], X_test_r[:, 1], label="test",
marker="*", c="r", s=50)
plt.xlabel("X comp. 1")
plt.ylabel("X comp. 2")
plt.title('X comp. 1 vs X comp. 2 (test corr = %.2f)'
% np.corrcoef(X_test_r[:, 0], X_test_r[:, 1])[0, 1])
plt.legend(loc="best")
plt.subplot(223)
plt.scatter(Y_train_r[:, 0], Y_train_r[:, 1], label="train",
marker="*", c="b", s=50)
plt.scatter(Y_test_r[:, 0], Y_test_r[:, 1], label="test",
marker="*", c="r", s=50)
plt.xlabel("Y comp. 1")
plt.ylabel("Y comp. 2")
plt.title('Y comp. 1 vs Y comp. 2 , (test corr = %.2f)'
% np.corrcoef(Y_test_r[:, 0], Y_test_r[:, 1])[0, 1])
plt.legend(loc="best")
plt.show()
#We can check the estimated projections
print('X projections: \n' + str(plsca.x_weights_))
print('Y projections: \n' + str(plsca.y_weights_))
X projections:
[[ 0.48433579 -0.25654367]
[-0.51415729 0.28837788]
[ 0.57083361 0.41523051]
[-0.1600194 0.72474008]
[-0.38678665 -0.39161076]]
Y projections:
[[ 0.36148438 0.39913339]
[-0.39571466 0.70730378]
[ 0.49905721 -0.35689321]
[-0.48904463 -0.31141709]
[-0.4738314 -0.34067659]]
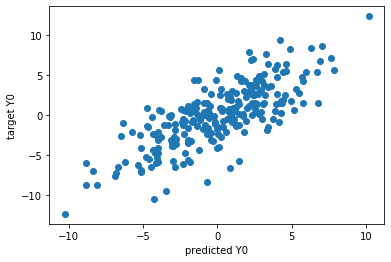
# Prediction for the training data
predicted_Y_train = plsca.predict(X_train)
plt.scatter(predicted_Y_train[:,dimension_to_plot], Y_train[:,dimension_to_plot])
plt.ylabel('target Y' + str(dimension_to_plot))
plt.xlabel('predicted Y' + str(dimension_to_plot))
plt.show()
plsca_4 = PLSCanonical(n_components=4)
plsca_4.fit(X_train, Y_train)
predicted_Y_train = plsca_4.predict(X_train)
print('X projections with 2 components: \n' + str(plsca.x_weights_))
print('Y projections with 2 components: \n' + str(plsca.y_weights_))
print('X projections with 4 components: \n' + str(plsca_4.x_weights_))
print('Y projections with 4 components: \n' + str(plsca_4.y_weights_))
X projections with 2 components:
[[ 0.48433579 -0.25654367]
[-0.51415729 0.28837788]
[ 0.57083361 0.41523051]
[-0.1600194 0.72474008]
[-0.38678665 -0.39161076]]
Y projections with 2 components:
[[ 0.36148438 0.39913339]
[-0.39571466 0.70730378]
[ 0.49905721 -0.35689321]
[-0.48904463 -0.31141709]
[-0.4738314 -0.34067659]]
X projections with 4 components:
[[ 0.48433579 -0.25654367 -0.42402831 0.54660349]
[-0.51415729 0.28837788 0.30201819 0.74306133]
[ 0.57083361 0.41523051 0.64183921 -0.06465157]
[-0.1600194 0.72474008 -0.51490022 -0.22931801]
[-0.38678665 -0.39161076 0.22782708 -0.30383862]]
Y projections with 4 components:
[[ 0.36148438 0.39913339 -0.5105896 0.60783454]
[-0.39571466 0.70730378 0.48505202 0.26714451]
[ 0.49905721 -0.35689321 0.58283628 0.50546537]
[-0.48904463 -0.31141709 0.17782666 0.30291833]
[-0.4738314 -0.34067659 -0.36428334 0.46034359]]
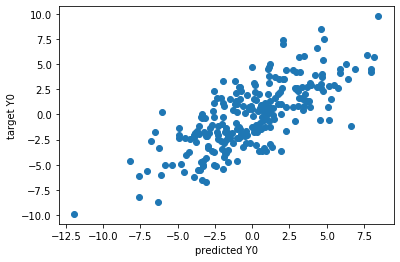
# We can also predict Y from X
predicted_Y_test = plsca.predict(X_test)
plt.scatter(predicted_Y_test[:,dimension_to_plot], Y_test[:,dimension_to_plot])
plt.ylabel('target Y' + str(dimension_to_plot))
plt.xlabel('predicted Y' + str(dimension_to_plot))
plt.show()
Exercise. Generate a synthetic dataset of 200 observations.
Each observation is composed by 3 modalities X1, X2, and X3, of dimensions respectively of 4, 7, and 9.
Chose the appropriate latent variable representation for the generative model.
These modalities are corrupted with Gaussian noise, with different noise variance for each modality.
Fit a PLS model to predict X3 from X1.
Into the guts of latent variable models¶
After playing with the builti-in implementation of PLS in scikit-learn, we are going to implement our own version based on the NIPALS method.
NIPALS for PLS¶
# Nipals method for PLS
n_components = 3
# Defining empty arrays where to store results
# Reconstruction from latent space to data
loading_x = np.ndarray([X.shape[1],n_components])
loading_y = np.ndarray([Y.shape[1],n_components])
# Projections into the latent space
weight_x = np.ndarray([X.shape[1],n_components])
weight_y = np.ndarray([Y.shape[1],n_components])
# Latent variables
scores_x = np.ndarray([X.shape[0],n_components])
scores_y = np.ndarray([Y.shape[0],n_components])
# Initialization of data matrices
current_X = X
current_Y = Y
for i in range(n_components):
# Initialization of current latent variables as a data column
t_x = current_X[:,0]
# NIPALS iterations
for _ in range(100):
# estimating Y weights given data Y and latent variables from X
w_y = current_Y.transpose().dot(t_x)/(t_x.transpose().dot(t_x))
# normalizing Y weights
w_y = w_y/np.sqrt(np.sum(w_y**2))
# estimating latent variables from Y given data Y and Y weights
t_y = current_Y.dot(w_y)
# estimating X weights given data X and latent variables from Y
w_x = current_X.transpose().dot(t_y)/(t_y.transpose().dot(t_y))
# normalizing X weights
w_x = w_x/np.sqrt(np.sum(w_x**2))
# estimating latent variables from X given data X and X weights
t_x = current_X.dot(w_x)
# Weights are such that X * weights = t
weight_x[:,i] = w_x
weight_y[:,i] = w_y
# Latent variables
scores_x[:,i] = t_x
scores_x[:,i] = t_y
# Loadings obtained by regressing X on t (X = t * loadings)
loading_x[:,i] = np.dot(current_X.T, t_x)/t_x.transpose().dot(t_x)
loading_y[:,i] = np.dot(current_Y.T, t_y)/t_y.transpose().dot(t_y)
# Deflation = current_data - current_reconstruction
current_X = current_X - t_x.reshape(len(t_x),1).dot(w_x.reshape(1,len(w_x)))
current_Y = current_Y - t_y.reshape(len(t_y),1).dot(w_y.reshape(1,len(w_y)))
print('The estimated projections for X are: \n' + str(weight_x))
print('\n The estimated projections for Y are: \n' + str(weight_y))
The estimated projections for X are:
[[ 0.36753226 0.32695545 0.31901594]
[-0.54017132 -0.51142438 -0.13635813]
[ 0.73596167 -0.54668695 -0.38095079]
[-0.07131382 -0.54068145 0.43213359]
[-0.16251074 0.20085364 -0.74011644]]
The estimated projections for Y are:
[[ 0.22469208 -0.22321827 0.22848154]
[-0.42360052 -0.82303817 -0.17028297]
[ 0.34143196 0.23277327 -0.37414229]
[-0.53070486 0.30658588 -0.6691619 ]
[-0.60979721 0.35299218 0.57536058]]
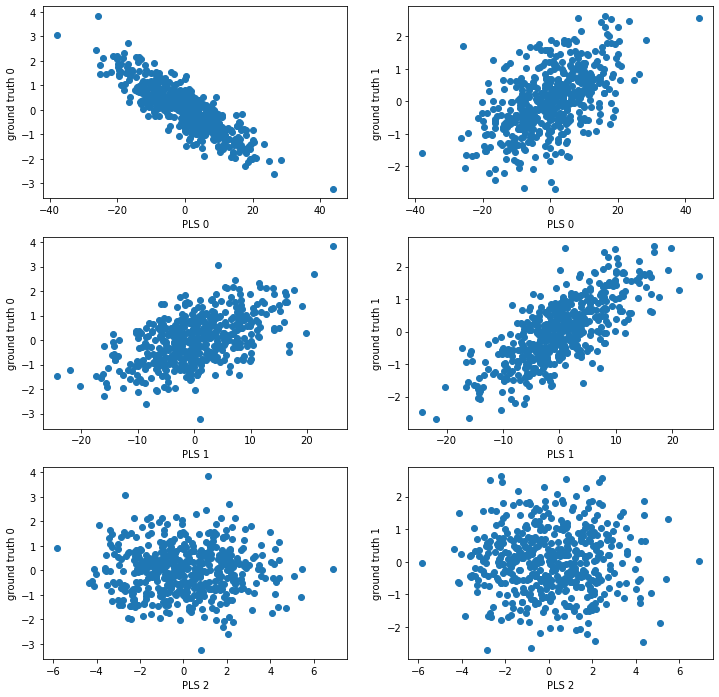
plt.figure(figsize=(12, 12))
plt.subplot(3,2,1)
plt.scatter(scores_x[:,0], latents[:,0])
plt.xlabel('PLS 0')
plt.ylabel('ground truth 0')
plt.subplot(3,2,2)
plt.scatter(scores_x[:,0], latents[:,1])
plt.xlabel('PLS 0')
plt.ylabel('ground truth 1')
plt.subplot(3,2,3)
plt.scatter(scores_x[:,1], latents[:,0])
plt.xlabel('PLS 1')
plt.ylabel('ground truth 0')
plt.subplot(3,2,4)
plt.scatter(scores_x[:,1], latents[:,1])
plt.xlabel('PLS 1')
plt.ylabel('ground truth 1')
plt.subplot(3,2,5)
plt.scatter(scores_x[:,2], latents[:,0])
plt.xlabel('PLS 2')
plt.ylabel('ground truth 0')
plt.subplot(3,2,6)
plt.scatter(scores_x[:,2], latents[:,1])
plt.xlabel('PLS 2')
plt.ylabel('ground truth 1')
plt.show()
Once that the PLS parameters are estimated, we can solve the regression problem for predicting Y from X. We adopt the scheme used in scikit-learn, where a rotation matrix is first estimated to accoung for non-cummutativity between projection (weights) and reconstruction (loadings).
# Identifying rotation from X to t
# t_x * loadings_x = X
# t_x * loadings_x.T * weight = X * weight
# t_x = X * weight * (loadings_x.T * weight)^-1 = X * rotations_x
rotations_x = weight_x.dot(np.linalg.pinv(loading_x.T.dot(weight_x)))
# Solving the regression from X to Y
# Y = t_x * loadings_y.T
# Y = X * rotations_x * loadings_y.T
regression_coef = np.dot(rotations_x, loading_y.T)
plt.figure(figsize=(12, 18))
for i in range(Y.shape[1]):
plt.subplot(Y.shape[1], 1, i+1)
plt.scatter(X.dot(regression_coef)[:,i], Y[:,i])
plt.xlabel('predicted dimension ' + str(i))
plt.ylabel('target dimension ' + str(i))
plt.show()

# Comparing with SVD of covariance matrix
eig_val_x, eig_vect, eig_val_y = np.linalg.svd(X.transpose().dot(Y))
print('Eigenvalues for X \n' + str(np.real(eig_val_x[:,:3])))
print('Estimated weights for X\n' + str(np.real(weight_x[:,:3])))
Eigenvalues for X
[[-0.36753226 0.32695545 0.31901594]
[ 0.54017132 -0.51142438 -0.13635813]
[-0.73596167 -0.54668695 -0.38095079]
[ 0.07131382 -0.54068145 0.43213359]
[ 0.16251074 0.20085364 -0.74011644]]
Estimated weights for X
[[ 0.36753226 0.32695545 0.31901594]
[-0.54017132 -0.51142438 -0.13635813]
[ 0.73596167 -0.54668695 -0.38095079]
[-0.07131382 -0.54068145 0.43213359]
[-0.16251074 0.20085364 -0.74011644]]
print('Eigenvalues for Y \n' + str(np.real(eig_val_y.T[:,:3])))
print('Estimated weights for Y\n' + str(np.real(weight_y[:,:3])))
Eigenvalues for Y
[[-0.22469208 -0.22321827 0.22848154]
[ 0.42360052 -0.82303817 -0.17028297]
[-0.34143196 0.23277327 -0.37414229]
[ 0.53070486 0.30658588 -0.6691619 ]
[ 0.60979721 0.35299218 0.57536058]]
Estimated weights for Y
[[ 0.22469208 -0.22321827 0.22848154]
[-0.42360052 -0.82303817 -0.17028297]
[ 0.34143196 0.23277327 -0.37414229]
[-0.53070486 0.30658588 -0.6691619 ]
[-0.60979721 0.35299218 0.57536058]]
# PLS in scikit-learn
plsca = PLSCanonical(n_components=3, scale = False)
plsca.fit(X, Y)
PLSCanonical(n_components=3, scale=False)
print(plsca.x_weights_)
print(plsca.y_weights_)
[[ 0.36745572 -0.32646087 -0.30267791]
[-0.5399922 0.51144303 0.11763542]
[ 0.73610243 0.54625149 0.37318486]
[-0.07130735 0.54144866 -0.38043117]
[-0.16264435 -0.20072864 0.78137902]]
[[ 0.22485955 0.22212135 -0.2169345 ]
[-0.42328296 0.82287418 0.1493648 ]
[ 0.34172183 -0.23372426 0.32376757]
[-0.53074024 -0.30704996 0.68434385]
[-0.60976283 -0.35303468 -0.59789433]]
NIPALS for CCA¶
import scipy
# Nipals method for CCA
# Defining empty arrays where to store results
# Reconstruction from latent space to data
loading_x_cca = np.ndarray([X.shape[1],n_components])
loading_y_cca = np.ndarray([Y.shape[1],n_components])
# Projections into the latent space
scores_x_cca = np.ndarray([X.shape[0],n_components])
scores_y_cca = np.ndarray([Y.shape[0],n_components])
# Latent variables
weight_x_cca = np.ndarray([X.shape[1],n_components])
weight_y_cca = np.ndarray([Y.shape[1],n_components])
# Initialization of data matrices
current_X = X
current_Y = Y
for i in range(n_components):
# Initialization of current latent variables as a data column
t_x = current_X[:,0]
# NIPALS iterations
for _ in range(500):
## CCA variant
# estimating Y weights given data Y and latent variables from X
Y_pinv = np.linalg.pinv(current_Y)
#Y_pinv = np.linalg.solve(current_Y.dot(current_Y.T),current_Y).T
w_y = Y_pinv.dot(t_x)
# normalizing Y weights
w_y = w_y/np.sqrt(np.sum(w_y**2))
# estimating latent variables from Y given data Y and Y weights
t_y = current_Y.dot(w_y)
## CCA variant
# estimating X weights given data X and latent variables from Y
X_pinv = np.linalg.pinv(current_X)
#X_pinv = np.linalg.solve(current_X.dot(current_X.T),current_X).T
w_x = X_pinv.dot(t_y)
# normalizing X weights
w_x = w_x/np.sqrt(np.sum(w_x**2))
# estimating latent variables from X given data X and X weights
t_x = current_X.dot(w_x)
# Weights are such that X * weights = t
weight_x_cca[:,i] = w_x
weight_y_cca[:,i] = w_y
# Latent dimensions
scores_x_cca[:,i] = t_x
scores_x_cca[:,i] = t_y
# Loadings obtained by regressing X on t (X = t * loadings)
loading_x_cca[:,i] = np.dot(current_X.T, t_x)/t_x.transpose().dot(t_x)
loading_y_cca[:,i] = np.dot(current_Y.T, t_y)/t_y.transpose().dot(t_y)
# Deflation = current_data - current_reconstruction
current_X = current_X - t_x.reshape(len(t_x),1).dot(w_x.reshape(1,len(w_x)))
current_Y = current_Y - t_y.reshape(len(t_y),1).dot(w_x.reshape(1,len(w_y)))
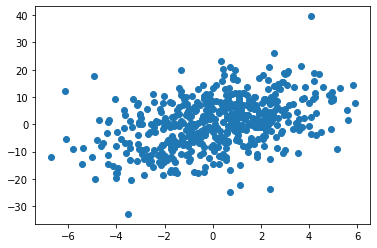
print(weight_x_cca)
plt.scatter(X.dot(weight_x_cca)[:,2], Y.dot(weight_y_cca)[:,2])
[[ 0.24391049 0.36361822 0.79534955]
[-0.47437693 -0.58135481 0.07701894]
[ 0.82921211 -0.45865491 -0.17520398]
[-0.04561038 -0.56190597 0.56872597]
[-0.16062744 0.06087473 -0.0856826 ]]
<matplotlib.collections.PathCollection at 0x7f7070df44d0>
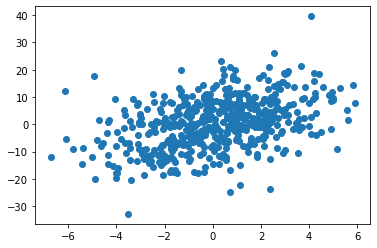
cca = CCA(n_components=3, scale = False)
cca.fit(X,Y)
print(cca.x_weights_)
plt.scatter(X.dot(weight_x_cca)[:,2], Y.dot(weight_y_cca)[:,2])
[[ 0.2415487 -0.32772785 -0.24927466]
[-0.47054284 0.58859583 0.10763174]
[ 0.83233244 0.44252343 0.28013453]
[-0.04077413 0.58734795 -0.35211385]
[-0.16063576 -0.07310815 0.85077496]]
<matplotlib.collections.PathCollection at 0x7f7070d38790>
Reduced Rank Regression¶
We finally review reduced rank regression through eigen-decomposition.
# Reduced Rank Regression
n_components = 2
Gamma = np.eye(n_components)
SYX = np.dot(Y.T,X)
SXX = np.dot(X.T,X)
U, S, V = np.linalg.svd(np.dot(SYX, np.dot(np.linalg.pinv(SXX), SYX.T)))
A = V[0:n_components, :].T
B = np.dot(np.dot(A.T,SYX), np.linalg.pinv(SXX))
A
array([[-0.24936409, -0.19522003],
[ 0.3233369 , -0.86712778],
[-0.31172187, 0.27190596],
[ 0.56300866, 0.2411439 ],
[ 0.64739595, 0.27909733]])
B
array([[-0.17847633, 0.34992334, -0.88917092, -0.05742634, 0.16716151],
[ 0.33903723, -0.60088957, -0.58551613, -0.63995952, 0.10694492]])
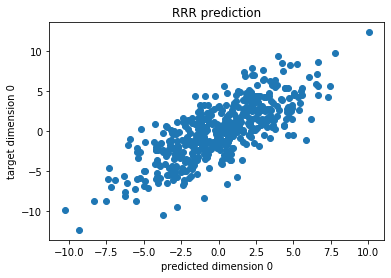
regression_coef_rrr = np.dot(A,B)
plt.scatter(np.dot(X,regression_coef)[:,0],Y[:,0])
plt.xlabel('predicted dimension 0')
plt.ylabel('target dimension 0')
plt.title('RRR prediction')
plt.show()
Sparsity in latent variable models¶
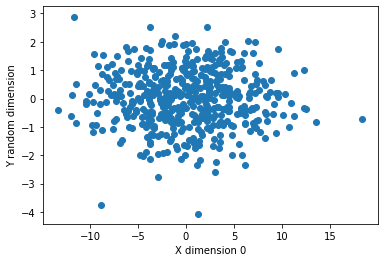
We now focus on the effect of spurious variables in mutivariate models. To explore this new setting, we are going to add spurious random features to our data matrices X and Y.
## Adding 3 random dimensions
## No association is expected from these features
X_ext = np.hstack([X,np.random.randn(n*3).reshape([n,3])])
Y_ext = np.hstack([Y,np.random.randn(n*3).reshape([n,3])])
plt.scatter(X_ext[:,0], Y_ext[:,-1])
plt.xlabel('X dimension 0')
plt.ylabel('Y random dimension')
plt.show()
from sklearn import linear_model
n_components = 3
#### Sparse PLS via regularization in NIPALS [Waaijenborg, et al 2007]
# Everything is as for the standard NIPALS algorithm, with the added sparse estimation step
loading_x_sparse = np.ndarray([X_ext.shape[1],n_components])
loading_y_sparse = np.ndarray([Y_ext.shape[1],n_components])
scores_x_sparse = np.ndarray([X_ext.shape[0],n_components])
scores_y_sparse = np.ndarray([Y_ext.shape[0],n_components])
weight_x_sparse = np.ndarray([X_ext.shape[1],n_components])
weight_y_sparse = np.ndarray([Y_ext.shape[1],n_components])
current_X = X_ext
current_Y = Y_ext
## Penalty parameter for regularization
penalty = 10
eps = 1e-4
for i in range(n_components):
t_x = current_X[:,0]
for _ in range(100):
w_y = current_Y.transpose().dot(t_x)/(t_x.transpose().dot(t_x))
w_y = w_y/np.sqrt(np.sum(w_y**2))
t_y = current_Y.dot(w_y)
w_x = current_X.transpose().dot(t_y)/(t_y.transpose().dot(t_y))
w_x = w_x/np.sqrt(np.sum(w_x**2))
t_x = current_X.dot(w_x)
## Estimating sparse model for the weights of X
lasso_x = linear_model.Lasso(alpha = penalty)
lasso_x.fit(t_x.reshape(-1, 1), current_X)
## Estimating sparse model for the weights of Y
lasso_y = linear_model.Lasso(alpha = penalty)
lasso_y.fit(t_y.reshape(-1, 1), current_Y)
# Replacing the original weights with the sparse estimation
w_x = (lasso_x.coef_ / (np.sqrt(np.sum(lasso_x.coef_**2) + eps))).reshape([X_ext.shape[1]])
w_y = (lasso_y.coef_ / (np.sqrt(np.sum(lasso_y.coef_**2) + eps))).reshape([Y_ext.shape[1]])
# Weights are such that X * weights = t
weight_x_sparse[:,i] = w_x
weight_y_sparse[:,i] = w_y
# Latent dimensions
scores_x_sparse[:,i] = t_x
scores_x_sparse[:,i] = t_y
# Loadings obtained by regressing X on t (X = t * loadings)
loading_x_sparse[:,i] = np.dot(current_X.T, t_x)/t_x.transpose().dot(t_x)
loading_y_sparse[:,i] = np.dot(current_Y.T, t_y)/t_y.transpose().dot(t_y)
# Deflation
current_X = current_X - t_x.reshape(len(t_x),1).dot(w_x.reshape(1,len(w_x)))
current_Y = current_Y - t_y.reshape(len(t_y),1).dot(w_y.reshape(1,len(w_y)))
We observe that the new weights are similar to the ones estimated before. However the parameters associated with the spurious dimension are entirely set to zero. This indicates that the model does not find these features necessary to explain the common variability between X and Y. There are also other weights which are set to zero, corresponding to the third latent dimension. This makes sense, as our synthetic data was indeed created with only two latent dimensions.
weight_x_sparse
array([[ 0.35947916, 0.09613335, 0. ],
[-0.57208323, -0.5017898 , 0. ],
[ 0.73260855, -0.60111564, 0. ],
[-0.01764855, -0.61404951, 0. ],
[-0.0795538 , 0. , 0. ],
[ 0. , 0. , 0. ],
[ 0. , 0. , 0. ],
[ 0. , 0. , -0. ]])
weight_y_sparse
array([[ 0.19008698, -0.03395428, -0. ],
[-0.3361836 , -0.95121052, 0. ],
[ 0.29093832, 0.05788278, 0. ],
[-0.56391994, 0.17865107, 0. ],
[-0.66936112, 0.24197983, 0. ],
[-0. , -0. , -0. ],
[ 0. , -0. , -0. ],
[-0. , -0. , -0. ]])
## Non-sparse parameters previously estimated
print(weight_x)
print(weight_y)
[[ 0.36753226 0.32695545 0.31901594]
[-0.54017132 -0.51142438 -0.13635813]
[ 0.73596167 -0.54668695 -0.38095079]
[-0.07131382 -0.54068145 0.43213359]
[-0.16251074 0.20085364 -0.74011644]]
[[ 0.22469208 -0.22321827 0.22848154]
[-0.42360052 -0.82303817 -0.17028297]
[ 0.34143196 0.23277327 -0.37414229]
[-0.53070486 0.30658588 -0.6691619 ]
[-0.60979721 0.35299218 0.57536058]]
## PLS result from scikit-learn PLS on the data augmented with spurious dimensions
plsca = PLSCanonical(n_components=3, scale = False)
plsca.fit(X_ext, Y_ext)
print(plsca.x_weights_)
print(plsca.y_weights_)
[[ 0.36744392 -0.32636735 -0.3736012 ]
[-0.53999014 0.51133222 0.13293972]
[ 0.73606624 0.54628291 0.34582048]
[-0.07131057 0.54141809 -0.49749784]
[-0.16262691 -0.20075143 0.52023542]
[ 0.00653338 -0.00825341 0.39402462]
[ 0.00339241 -0.00798747 0.07331524]
[ 0.0038984 -0.00566521 0.21066051]]
[[ 0.22481823 0.22219588 -0.39318404]
[-0.4232868 0.82282067 0.19587236]
[ 0.34171379 -0.2337191 0.39240653]
[-0.53068906 -0.30708105 0.46282095]
[-0.6097158 -0.353037 -0.46080397]
[-0.00986828 0.00097623 -0.2131351 ]
[ 0.00469737 0.00268147 -0.28959681]
[-0.00361132 0.00533588 -0.31180287]]
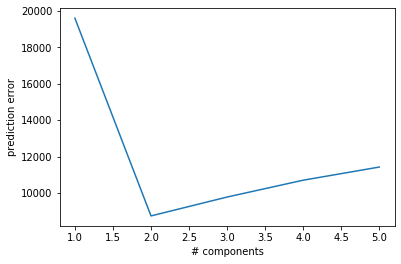
Cross-validating components¶
In addition to sparsity, the optimal number of components in latent variable models can be identified by cross-validation. A common strategy is to train the model on a subset of the data and to quantify the predicted residual error sum of squares (PRESS) in non-overlapping testing data. We can finally choose the number of latent dimensions leading to the lowest average PRESS.
n_cross_valid_run = 200
# max number of components to test
n_components = 5
rep_results = []
for i in range(n_components):
rep_results.append([])
for k in range(n_components):
for i in range(n_cross_valid_run):
# Sampling disjoint set of indices for splitting the data
batch1_idx = np.random.choice(range(X_ext.shape[0]), size = int(X_ext.shape[0]/2), replace = False)
batch2_idx = np.where(np.in1d(range(X_ext.shape[0]), batch1_idx, assume_unique=True, invert = True))[0]
# Creating independent data batches for X
X_1 = X_ext[batch1_idx, :]
X_2 = X_ext[batch2_idx, :]
# Creating independent data batches for Y
Y_1 = Y_ext[batch1_idx, :]
Y_2 = Y_ext[batch2_idx, :]
# Creating a model for each data batch
plsca1 = PLSCanonical(n_components = k+1, scale = False)
plsca2 = PLSCanonical(n_components = k+1, scale = False)
# Fitting a model for each data batch
plsca1.fit(X_1,Y_1)
plsca2.fit(X_2,Y_2)
# Quantifying the prediction error on the unseen data batch
err1 = np.sum((plsca1.predict(X_2) - Y_2)**2)
err2 = np.sum((plsca2.predict(X_1) - Y_1)**2)
rep_results[k].append(np.mean([err1,err2]))
plt.plot(range(1,n_components+1),np.mean(rep_results, 1))
plt.xlabel('# components')
plt.ylabel('prediction error')
plt.show()
Multi-channel Variational Autoencoder¶
The last part of this tutorial concerns the use of the multi-channel variational autoencoder (https://gitlab.inria.fr/epione_ML/mcvae), a more advanced methods for the joint analysis and prediction of several modalities.
VAE¶
The Variational Autoencoer is a latent variable model composed by one encoder and one decoder associated to a single channel. The latent distribution and the decoding distribution are implemented as follows:
They are Gaussians with moments parametrized by Neural Networks (or a linear transformation layer in a simple case).

Exercise¶
Why is convenient to use \(\log\) values for the parametrization the variance networks output (W_logvar, W_out_logvar)?
Sparse VAE¶
To favour sparsity in the latent space we implement the latent distribution as follows:
where:
Tha parameter \(\alpha_i\) represents the odds of pruning the \(i\)-th latent dimension according to:

MCVAE¶
The MultiChannel VAE is built by stacking multiple VAEs and allowing the decoding distributions to be computed from every input channel.

Exercise¶
Sketch the Sparse MCVAE with 3 channels. [Solution]
import torch
from mcvae.models import Mcvae
from mcvae.models.utils import DEVICE, load_or_fit
from mcvae.diagnostics import *
from mcvae.plot import lsplom
print(f"Running on {DEVICE}") # cpu or gpu
FORCE_REFIT = False # Set this to 'True' if ou want to refit the models instead of loading them from file.
Running on cpu
### To initialization of the mcvae model you should provide:
# 1 - a list with the different data channels
data = [X, Y]
data = [torch.Tensor(_) for _ in data] #warning: data matrices must be converted to type torch.Tensor
# 1 - a dictionary with the data and model characteristics
init_dict = {
'data': data,
'lat_dim': n_components,
}
# Here we initialize an instance of the model
# Multi-Channel VAE
torch.manual_seed(24)
model = Mcvae(**init_dict)
model.to(DEVICE)
print(model)
Mcvae(
(vae): ModuleList(
(0): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=5, out_features=5, bias=True)
(W_logvar): Linear(in_features=5, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=5, bias=True)
)
(1): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=5, out_features=5, bias=True)
(W_logvar): Linear(in_features=5, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=5, bias=True)
)
)
)
###################
## Model Fitting ##
###################
# Set up the optimizer
adam_lr = 1e-2
n_epochs = 5000
model.optimizer = torch.optim.Adam(model.parameters(), lr=adam_lr)
# We will use the custom routine "load_or_fit" to fit the model
help(load_or_fit)
Help on function load_or_fit in module mcvae.models.utils:
load_or_fit(model, data, epochs, ptfile, init_loss=True, minibatch=False, force_fit=False)
Routine to train or load a model.
:param model: model to optimize
:param data: training data
:param epochs: number of training epochs
:param ptfile: path to *.pt file where to save the trained model
:param force_fit: force the training even if the model is already trained
# Fit the model
load_or_fit(model=model, data=data, epochs=n_epochs, ptfile='model.pt', force_fit=True)
Creating model.pt.running
Created: 2021-01-08 18:02:05.267851
Start fitting: 2021-01-08 18:02:05.268239
Model destination: model.pt
====> Epoch: 0/5000 (0%) Loss: 4262660.5000 LL: -1298590.0000 KL: 2964070.5000 LL/KL: -0.4381
====> Epoch: 10/5000 (0%) Loss: 43945.0391 LL: -34668.4375 KL: 9276.6035 LL/KL: -3.7372
====> Epoch: 20/5000 (0%) Loss: 19446.6035 LL: -17842.4414 KL: 1604.1619 LL/KL: -11.1226
====> Epoch: 30/5000 (1%) Loss: 12697.3916 LL: -11797.3516 KL: 900.0399 LL/KL: -13.1076
====> Epoch: 40/5000 (1%) Loss: 6696.4473 LL: -5948.7456 KL: 747.7017 LL/KL: -7.9560
====> Epoch: 50/5000 (1%) Loss: 14101.9600 LL: -13389.3281 KL: 712.6315 LL/KL: -18.7886
====> Epoch: 60/5000 (1%) Loss: 6858.8511 LL: -6148.5029 KL: 710.3480 LL/KL: -8.6556
====> Epoch: 70/5000 (1%) Loss: 7487.5254 LL: -6770.8442 KL: 716.6814 LL/KL: -9.4475
====> Epoch: 80/5000 (2%) Loss: 3859.8472 LL: -3138.4307 KL: 721.4165 LL/KL: -4.3504
====> Epoch: 90/5000 (2%) Loss: 4518.0630 LL: -3797.2717 KL: 720.7911 LL/KL: -5.2682
====> Epoch: 100/5000 (2%) Loss: 5719.1602 LL: -5000.9023 KL: 718.2576 LL/KL: -6.9625
====> Epoch: 110/5000 (2%) Loss: 2709.6421 LL: -1994.7473 KL: 714.8947 LL/KL: -2.7903
====> Epoch: 120/5000 (2%) Loss: 7239.8066 LL: -6530.8994 KL: 708.9070 LL/KL: -9.2126
====> Epoch: 130/5000 (3%) Loss: 2872.6157 LL: -2171.9895 KL: 700.6263 LL/KL: -3.1001
====> Epoch: 140/5000 (3%) Loss: 2293.5227 LL: -1601.2192 KL: 692.3034 LL/KL: -2.3129
====> Epoch: 150/5000 (3%) Loss: 6731.0962 LL: -6047.7144 KL: 683.3818 LL/KL: -8.8497
====> Epoch: 160/5000 (3%) Loss: 3181.1064 LL: -2508.8794 KL: 672.2271 LL/KL: -3.7322
====> Epoch: 170/5000 (3%) Loss: 6107.2334 LL: -5445.0718 KL: 662.1615 LL/KL: -8.2232
====> Epoch: 180/5000 (4%) Loss: 4395.3936 LL: -3742.2568 KL: 653.1368 LL/KL: -5.7297
====> Epoch: 190/5000 (4%) Loss: 2763.1292 LL: -2120.5781 KL: 642.5511 LL/KL: -3.3002
====> Epoch: 200/5000 (4%) Loss: 2477.9043 LL: -1844.8848 KL: 633.0195 LL/KL: -2.9144
====> Epoch: 210/5000 (4%) Loss: 2105.9983 LL: -1484.8384 KL: 621.1599 LL/KL: -2.3904
====> Epoch: 220/5000 (4%) Loss: 13323.0703 LL: -12711.7891 KL: 611.2809 LL/KL: -20.7953
====> Epoch: 230/5000 (5%) Loss: 5057.8389 LL: -4457.0781 KL: 600.7610 LL/KL: -7.4191
====> Epoch: 240/5000 (5%) Loss: 4228.7827 LL: -3635.3999 KL: 593.3828 LL/KL: -6.1266
====> Epoch: 250/5000 (5%) Loss: 3765.3745 LL: -3181.7815 KL: 583.5930 LL/KL: -5.4521
====> Epoch: 260/5000 (5%) Loss: 3960.7463 LL: -3385.7822 KL: 574.9642 LL/KL: -5.8887
====> Epoch: 270/5000 (5%) Loss: 2081.4968 LL: -1515.2067 KL: 566.2901 LL/KL: -2.6757
====> Epoch: 280/5000 (6%) Loss: 6944.0654 LL: -6382.9033 KL: 561.1620 LL/KL: -11.3744
====> Epoch: 290/5000 (6%) Loss: 3887.6899 LL: -3335.7651 KL: 551.9247 LL/KL: -6.0439
====> Epoch: 300/5000 (6%) Loss: 3377.1025 LL: -2831.6406 KL: 545.4619 LL/KL: -5.1913
====> Epoch: 310/5000 (6%) Loss: 3452.5525 LL: -2914.7649 KL: 537.7876 LL/KL: -5.4199
====> Epoch: 320/5000 (6%) Loss: 2786.2290 LL: -2257.6572 KL: 528.5719 LL/KL: -4.2712
====> Epoch: 330/5000 (7%) Loss: 1775.6956 LL: -1252.7754 KL: 522.9201 LL/KL: -2.3957
====> Epoch: 340/5000 (7%) Loss: 3147.1799 LL: -2630.1743 KL: 517.0056 LL/KL: -5.0873
====> Epoch: 350/5000 (7%) Loss: 2116.6458 LL: -1609.1597 KL: 507.4861 LL/KL: -3.1708
====> Epoch: 360/5000 (7%) Loss: 3679.0774 LL: -3177.3794 KL: 501.6980 LL/KL: -6.3333
====> Epoch: 370/5000 (7%) Loss: 2289.3469 LL: -1792.4320 KL: 496.9149 LL/KL: -3.6071
====> Epoch: 380/5000 (8%) Loss: 3934.2031 LL: -3446.0605 KL: 488.1425 LL/KL: -7.0595
====> Epoch: 390/5000 (8%) Loss: 2178.9221 LL: -1699.2437 KL: 479.6784 LL/KL: -3.5425
====> Epoch: 400/5000 (8%) Loss: 3150.6499 LL: -2679.0728 KL: 471.5771 LL/KL: -5.6811
====> Epoch: 410/5000 (8%) Loss: 2006.5717 LL: -1541.8043 KL: 464.7673 LL/KL: -3.3174
====> Epoch: 420/5000 (8%) Loss: 2842.1255 LL: -2385.0315 KL: 457.0941 LL/KL: -5.2178
====> Epoch: 430/5000 (9%) Loss: 2685.0171 LL: -2235.1396 KL: 449.8773 LL/KL: -4.9683
====> Epoch: 440/5000 (9%) Loss: 3580.0781 LL: -3133.2732 KL: 446.8050 LL/KL: -7.0126
====> Epoch: 450/5000 (9%) Loss: 2881.6396 LL: -2439.3345 KL: 442.3052 LL/KL: -5.5150
====> Epoch: 460/5000 (9%) Loss: 3728.0725 LL: -3290.8694 KL: 437.2030 LL/KL: -7.5271
====> Epoch: 470/5000 (9%) Loss: 2724.9758 LL: -2292.2390 KL: 432.7368 LL/KL: -5.2971
====> Epoch: 480/5000 (10%) Loss: 2711.6714 LL: -2287.2346 KL: 424.4366 LL/KL: -5.3889
====> Epoch: 490/5000 (10%) Loss: 1880.4370 LL: -1461.4816 KL: 418.9554 LL/KL: -3.4884
====> Epoch: 500/5000 (10%) Loss: 2494.4944 LL: -2080.9089 KL: 413.5854 LL/KL: -5.0314
====> Epoch: 510/5000 (10%) Loss: 1736.9312 LL: -1324.5104 KL: 412.4208 LL/KL: -3.2116
====> Epoch: 520/5000 (10%) Loss: 2838.1016 LL: -2429.9229 KL: 408.1786 LL/KL: -5.9531
====> Epoch: 530/5000 (11%) Loss: 3567.1365 LL: -3164.5684 KL: 402.5682 LL/KL: -7.8610
====> Epoch: 540/5000 (11%) Loss: 1835.9888 LL: -1439.1138 KL: 396.8751 LL/KL: -3.6261
====> Epoch: 550/5000 (11%) Loss: 2106.6096 LL: -1714.1101 KL: 392.4995 LL/KL: -4.3672
====> Epoch: 560/5000 (11%) Loss: 1757.2501 LL: -1368.5223 KL: 388.7278 LL/KL: -3.5205
====> Epoch: 570/5000 (11%) Loss: 1735.3756 LL: -1351.3695 KL: 384.0061 LL/KL: -3.5191
====> Epoch: 580/5000 (12%) Loss: 1979.7140 LL: -1599.3445 KL: 380.3695 LL/KL: -4.2047
====> Epoch: 590/5000 (12%) Loss: 2113.2715 LL: -1738.4941 KL: 374.7774 LL/KL: -4.6387
====> Epoch: 600/5000 (12%) Loss: 1582.7756 LL: -1211.4095 KL: 371.3661 LL/KL: -3.2620
====> Epoch: 610/5000 (12%) Loss: 2550.9966 LL: -2183.7983 KL: 367.1982 LL/KL: -5.9472
====> Epoch: 620/5000 (12%) Loss: 3524.0396 LL: -3160.2539 KL: 363.7857 LL/KL: -8.6871
====> Epoch: 630/5000 (13%) Loss: 2121.2957 LL: -1763.3776 KL: 357.9180 LL/KL: -4.9268
====> Epoch: 640/5000 (13%) Loss: 1560.4982 LL: -1205.3318 KL: 355.1664 LL/KL: -3.3937
====> Epoch: 650/5000 (13%) Loss: 2421.0500 LL: -2070.0435 KL: 351.0065 LL/KL: -5.8975
====> Epoch: 660/5000 (13%) Loss: 2265.9092 LL: -1918.2366 KL: 347.6726 LL/KL: -5.5174
====> Epoch: 670/5000 (13%) Loss: 1571.7317 LL: -1226.0120 KL: 345.7198 LL/KL: -3.5463
====> Epoch: 680/5000 (14%) Loss: 4609.3799 LL: -4268.1899 KL: 341.1900 LL/KL: -12.5097
====> Epoch: 690/5000 (14%) Loss: 1591.5065 LL: -1255.7960 KL: 335.7104 LL/KL: -3.7407
====> Epoch: 700/5000 (14%) Loss: 3109.3455 LL: -2776.6707 KL: 332.6749 LL/KL: -8.3465
====> Epoch: 710/5000 (14%) Loss: 1970.4255 LL: -1642.4529 KL: 327.9727 LL/KL: -5.0079
====> Epoch: 720/5000 (14%) Loss: 1787.7649 LL: -1462.7594 KL: 325.0055 LL/KL: -4.5007
====> Epoch: 730/5000 (15%) Loss: 2275.4277 LL: -1952.7251 KL: 322.7026 LL/KL: -6.0512
====> Epoch: 740/5000 (15%) Loss: 2411.7817 LL: -2093.2559 KL: 318.5259 LL/KL: -6.5717
====> Epoch: 750/5000 (15%) Loss: 2171.4382 LL: -1856.8210 KL: 314.6172 LL/KL: -5.9018
====> Epoch: 760/5000 (15%) Loss: 1972.3674 LL: -1660.2032 KL: 312.1642 LL/KL: -5.3184
====> Epoch: 770/5000 (15%) Loss: 1599.5530 LL: -1289.0352 KL: 310.5179 LL/KL: -4.1512
====> Epoch: 780/5000 (16%) Loss: 1588.9763 LL: -1282.9235 KL: 306.0529 LL/KL: -4.1918
====> Epoch: 790/5000 (16%) Loss: 1825.2235 LL: -1524.0449 KL: 301.1786 LL/KL: -5.0603
====> Epoch: 800/5000 (16%) Loss: 2668.4998 LL: -2369.5227 KL: 298.9771 LL/KL: -7.9254
====> Epoch: 810/5000 (16%) Loss: 2814.1914 LL: -2516.2664 KL: 297.9249 LL/KL: -8.4460
====> Epoch: 820/5000 (16%) Loss: 1627.4493 LL: -1334.5055 KL: 292.9438 LL/KL: -4.5555
====> Epoch: 830/5000 (17%) Loss: 1940.0685 LL: -1649.6368 KL: 290.4317 LL/KL: -5.6799
====> Epoch: 840/5000 (17%) Loss: 2364.3738 LL: -2075.8496 KL: 288.5241 LL/KL: -7.1947
====> Epoch: 850/5000 (17%) Loss: 1524.1296 LL: -1236.8584 KL: 287.2712 LL/KL: -4.3055
====> Epoch: 860/5000 (17%) Loss: 1875.9878 LL: -1594.3328 KL: 281.6550 LL/KL: -5.6606
====> Epoch: 870/5000 (17%) Loss: 1628.6495 LL: -1348.7826 KL: 279.8669 LL/KL: -4.8194
====> Epoch: 880/5000 (18%) Loss: 1761.2710 LL: -1481.9734 KL: 279.2976 LL/KL: -5.3061
====> Epoch: 890/5000 (18%) Loss: 3350.5596 LL: -3075.5371 KL: 275.0224 LL/KL: -11.1829
====> Epoch: 900/5000 (18%) Loss: 2062.5210 LL: -1790.2250 KL: 272.2959 LL/KL: -6.5746
====> Epoch: 910/5000 (18%) Loss: 2666.9690 LL: -2398.1233 KL: 268.8458 LL/KL: -8.9201
====> Epoch: 920/5000 (18%) Loss: 1707.1511 LL: -1441.3044 KL: 265.8467 LL/KL: -5.4216
====> Epoch: 930/5000 (19%) Loss: 1457.5961 LL: -1192.8110 KL: 264.7851 LL/KL: -4.5048
====> Epoch: 940/5000 (19%) Loss: 2139.0674 LL: -1878.0316 KL: 261.0356 LL/KL: -7.1945
====> Epoch: 950/5000 (19%) Loss: 2519.4126 LL: -2258.8013 KL: 260.6112 LL/KL: -8.6673
====> Epoch: 960/5000 (19%) Loss: 2455.6077 LL: -2196.4492 KL: 259.1585 LL/KL: -8.4753
====> Epoch: 970/5000 (19%) Loss: 1682.2816 LL: -1428.2273 KL: 254.0543 LL/KL: -5.6217
====> Epoch: 980/5000 (20%) Loss: 1229.0485 LL: -975.1719 KL: 253.8765 LL/KL: -3.8411
====> Epoch: 990/5000 (20%) Loss: 1272.7069 LL: -1023.4662 KL: 249.2407 LL/KL: -4.1063
====> Epoch: 1000/5000 (20%) Loss: 2016.0963 LL: -1769.5736 KL: 246.5227 LL/KL: -7.1781
====> Epoch: 1010/5000 (20%) Loss: 1465.2620 LL: -1219.1506 KL: 246.1114 LL/KL: -4.9537
====> Epoch: 1020/5000 (20%) Loss: 1232.1704 LL: -988.1989 KL: 243.9716 LL/KL: -4.0505
====> Epoch: 1030/5000 (21%) Loss: 1321.5819 LL: -1079.4614 KL: 242.1205 LL/KL: -4.4584
====> Epoch: 1040/5000 (21%) Loss: 3451.2773 LL: -3211.1797 KL: 240.0978 LL/KL: -13.3745
====> Epoch: 1050/5000 (21%) Loss: 1498.3079 LL: -1260.6826 KL: 237.6252 LL/KL: -5.3053
====> Epoch: 1060/5000 (21%) Loss: 2068.7151 LL: -1832.0361 KL: 236.6789 LL/KL: -7.7406
====> Epoch: 1070/5000 (21%) Loss: 1710.2220 LL: -1476.9397 KL: 233.2823 LL/KL: -6.3311
====> Epoch: 1080/5000 (22%) Loss: 1126.5889 LL: -894.3732 KL: 232.2156 LL/KL: -3.8515
====> Epoch: 1090/5000 (22%) Loss: 2401.8350 LL: -2169.5151 KL: 232.3199 LL/KL: -9.3385
====> Epoch: 1100/5000 (22%) Loss: 2254.7361 LL: -2026.5315 KL: 228.2046 LL/KL: -8.8803
====> Epoch: 1110/5000 (22%) Loss: 1205.6593 LL: -977.9169 KL: 227.7423 LL/KL: -4.2940
====> Epoch: 1120/5000 (22%) Loss: 1547.9728 LL: -1322.4303 KL: 225.5425 LL/KL: -5.8633
====> Epoch: 1130/5000 (23%) Loss: 1492.6935 LL: -1270.3347 KL: 222.3587 LL/KL: -5.7130
====> Epoch: 1140/5000 (23%) Loss: 2329.0613 LL: -2105.9451 KL: 223.1162 LL/KL: -9.4388
====> Epoch: 1150/5000 (23%) Loss: 1332.1718 LL: -1112.1809 KL: 219.9908 LL/KL: -5.0556
====> Epoch: 1160/5000 (23%) Loss: 1134.4077 LL: -917.7589 KL: 216.6489 LL/KL: -4.2362
====> Epoch: 1170/5000 (23%) Loss: 2556.1628 LL: -2340.0276 KL: 216.1352 LL/KL: -10.8267
====> Epoch: 1180/5000 (24%) Loss: 2171.3357 LL: -1957.7233 KL: 213.6124 LL/KL: -9.1648
====> Epoch: 1190/5000 (24%) Loss: 1463.3451 LL: -1251.0682 KL: 212.2769 LL/KL: -5.8936
====> Epoch: 1200/5000 (24%) Loss: 1966.2485 LL: -1756.8313 KL: 209.4172 LL/KL: -8.3891
====> Epoch: 1210/5000 (24%) Loss: 1936.5503 LL: -1729.0808 KL: 207.4695 LL/KL: -8.3341
====> Epoch: 1220/5000 (24%) Loss: 1112.4226 LL: -904.4305 KL: 207.9921 LL/KL: -4.3484
====> Epoch: 1230/5000 (25%) Loss: 1140.7767 LL: -936.2104 KL: 204.5663 LL/KL: -4.5766
====> Epoch: 1240/5000 (25%) Loss: 1180.8647 LL: -977.3467 KL: 203.5181 LL/KL: -4.8023
====> Epoch: 1250/5000 (25%) Loss: 1231.2023 LL: -1028.8901 KL: 202.3122 LL/KL: -5.0857
====> Epoch: 1260/5000 (25%) Loss: 1255.2245 LL: -1054.3956 KL: 200.8289 LL/KL: -5.2502
====> Epoch: 1270/5000 (25%) Loss: 1271.5682 LL: -1072.6709 KL: 198.8973 LL/KL: -5.3931
====> Epoch: 1280/5000 (26%) Loss: 1317.8157 LL: -1120.7584 KL: 197.0573 LL/KL: -5.6875
====> Epoch: 1290/5000 (26%) Loss: 1179.8812 LL: -984.6975 KL: 195.1837 LL/KL: -5.0450
====> Epoch: 1300/5000 (26%) Loss: 1040.5862 LL: -846.2059 KL: 194.3803 LL/KL: -4.3534
====> Epoch: 1310/5000 (26%) Loss: 1151.3981 LL: -958.2407 KL: 193.1574 LL/KL: -4.9609
====> Epoch: 1320/5000 (26%) Loss: 1460.1351 LL: -1268.0066 KL: 192.1286 LL/KL: -6.5998
====> Epoch: 1330/5000 (27%) Loss: 1186.6499 LL: -996.7165 KL: 189.9334 LL/KL: -5.2477
====> Epoch: 1340/5000 (27%) Loss: 1259.4811 LL: -1069.1423 KL: 190.3388 LL/KL: -5.6170
====> Epoch: 1350/5000 (27%) Loss: 1281.3859 LL: -1092.9219 KL: 188.4640 LL/KL: -5.7991
====> Epoch: 1360/5000 (27%) Loss: 1176.5123 LL: -990.7215 KL: 185.7908 LL/KL: -5.3325
====> Epoch: 1370/5000 (27%) Loss: 2040.7468 LL: -1854.4304 KL: 186.3164 LL/KL: -9.9531
====> Epoch: 1380/5000 (28%) Loss: 1331.0305 LL: -1146.7010 KL: 184.3295 LL/KL: -6.2209
====> Epoch: 1390/5000 (28%) Loss: 1434.0869 LL: -1249.6487 KL: 184.4382 LL/KL: -6.7754
====> Epoch: 1400/5000 (28%) Loss: 1721.0398 LL: -1539.9001 KL: 181.1397 LL/KL: -8.5012
====> Epoch: 1410/5000 (28%) Loss: 1440.5950 LL: -1259.7344 KL: 180.8607 LL/KL: -6.9652
====> Epoch: 1420/5000 (28%) Loss: 1870.1147 LL: -1690.8724 KL: 179.2423 LL/KL: -9.4334
====> Epoch: 1430/5000 (29%) Loss: 1146.2024 LL: -968.6732 KL: 177.5292 LL/KL: -5.4564
====> Epoch: 1440/5000 (29%) Loss: 1291.2157 LL: -1114.5911 KL: 176.6246 LL/KL: -6.3105
====> Epoch: 1450/5000 (29%) Loss: 1167.1429 LL: -992.8992 KL: 174.2438 LL/KL: -5.6983
====> Epoch: 1460/5000 (29%) Loss: 1541.9700 LL: -1368.6398 KL: 173.3302 LL/KL: -7.8961
====> Epoch: 1470/5000 (29%) Loss: 1334.2880 LL: -1160.0168 KL: 174.2711 LL/KL: -6.6564
====> Epoch: 1480/5000 (30%) Loss: 1559.2811 LL: -1387.6062 KL: 171.6749 LL/KL: -8.0828
====> Epoch: 1490/5000 (30%) Loss: 1385.4377 LL: -1215.6008 KL: 169.8369 LL/KL: -7.1575
====> Epoch: 1500/5000 (30%) Loss: 2009.4011 LL: -1839.0745 KL: 170.3267 LL/KL: -10.7973
====> Epoch: 1510/5000 (30%) Loss: 1121.4117 LL: -953.1074 KL: 168.3044 LL/KL: -5.6630
====> Epoch: 1520/5000 (30%) Loss: 2043.5652 LL: -1876.7042 KL: 166.8610 LL/KL: -11.2471
====> Epoch: 1530/5000 (31%) Loss: 1153.7765 LL: -988.9729 KL: 164.8036 LL/KL: -6.0009
====> Epoch: 1540/5000 (31%) Loss: 2205.5872 LL: -2042.0969 KL: 163.4903 LL/KL: -12.4906
====> Epoch: 1550/5000 (31%) Loss: 1116.8275 LL: -953.1720 KL: 163.6555 LL/KL: -5.8243
====> Epoch: 1560/5000 (31%) Loss: 1190.0483 LL: -1028.2065 KL: 161.8418 LL/KL: -6.3532
====> Epoch: 1570/5000 (31%) Loss: 1283.1998 LL: -1121.2623 KL: 161.9375 LL/KL: -6.9240
====> Epoch: 1580/5000 (32%) Loss: 1140.5878 LL: -979.8543 KL: 160.7335 LL/KL: -6.0961
====> Epoch: 1590/5000 (32%) Loss: 1143.3615 LL: -984.2577 KL: 159.1038 LL/KL: -6.1863
====> Epoch: 1600/5000 (32%) Loss: 1675.2139 LL: -1516.7173 KL: 158.4965 LL/KL: -9.5694
====> Epoch: 1610/5000 (32%) Loss: 1085.5797 LL: -927.8647 KL: 157.7150 LL/KL: -5.8832
====> Epoch: 1620/5000 (32%) Loss: 1090.6754 LL: -934.8406 KL: 155.8348 LL/KL: -5.9989
====> Epoch: 1630/5000 (33%) Loss: 866.0853 LL: -710.2181 KL: 155.8672 LL/KL: -4.5566
====> Epoch: 1640/5000 (33%) Loss: 1217.4338 LL: -1061.5758 KL: 155.8581 LL/KL: -6.8112
====> Epoch: 1650/5000 (33%) Loss: 915.8037 LL: -762.0650 KL: 153.7387 LL/KL: -4.9569
====> Epoch: 1660/5000 (33%) Loss: 946.9049 LL: -793.6376 KL: 153.2673 LL/KL: -5.1781
====> Epoch: 1670/5000 (33%) Loss: 1101.5500 LL: -950.2353 KL: 151.3148 LL/KL: -6.2799
====> Epoch: 1680/5000 (34%) Loss: 1153.0992 LL: -1001.4298 KL: 151.6694 LL/KL: -6.6027
====> Epoch: 1690/5000 (34%) Loss: 1225.5017 LL: -1074.3660 KL: 151.1357 LL/KL: -7.1086
====> Epoch: 1700/5000 (34%) Loss: 972.7237 LL: -823.2496 KL: 149.4741 LL/KL: -5.5076
====> Epoch: 1710/5000 (34%) Loss: 937.8472 LL: -788.2142 KL: 149.6330 LL/KL: -5.2676
====> Epoch: 1720/5000 (34%) Loss: 1087.0841 LL: -941.2687 KL: 145.8153 LL/KL: -6.4552
====> Epoch: 1730/5000 (35%) Loss: 1199.5356 LL: -1052.0037 KL: 147.5320 LL/KL: -7.1307
====> Epoch: 1740/5000 (35%) Loss: 951.2284 LL: -805.0386 KL: 146.1898 LL/KL: -5.5068
====> Epoch: 1750/5000 (35%) Loss: 982.2732 LL: -836.9806 KL: 145.2926 LL/KL: -5.7607
====> Epoch: 1760/5000 (35%) Loss: 1210.2473 LL: -1065.9546 KL: 144.2927 LL/KL: -7.3874
====> Epoch: 1770/5000 (35%) Loss: 902.0007 LL: -758.2146 KL: 143.7861 LL/KL: -5.2732
====> Epoch: 1780/5000 (36%) Loss: 1000.2294 LL: -858.0259 KL: 142.2035 LL/KL: -6.0338
====> Epoch: 1790/5000 (36%) Loss: 989.3272 LL: -847.5911 KL: 141.7361 LL/KL: -5.9801
====> Epoch: 1800/5000 (36%) Loss: 1184.1068 LL: -1042.6858 KL: 141.4210 LL/KL: -7.3729
====> Epoch: 1810/5000 (36%) Loss: 987.6963 LL: -847.6875 KL: 140.0088 LL/KL: -6.0545
====> Epoch: 1820/5000 (36%) Loss: 1236.5851 LL: -1095.5911 KL: 140.9940 LL/KL: -7.7705
====> Epoch: 1830/5000 (37%) Loss: 950.8773 LL: -813.3464 KL: 137.5309 LL/KL: -5.9139
====> Epoch: 1840/5000 (37%) Loss: 1054.3411 LL: -914.6507 KL: 139.6904 LL/KL: -6.5477
====> Epoch: 1850/5000 (37%) Loss: 1188.7308 LL: -1052.3862 KL: 136.3446 LL/KL: -7.7186
====> Epoch: 1860/5000 (37%) Loss: 905.0150 LL: -767.8563 KL: 137.1587 LL/KL: -5.5983
====> Epoch: 1870/5000 (37%) Loss: 1002.6384 LL: -866.9100 KL: 135.7284 LL/KL: -6.3871
====> Epoch: 1880/5000 (38%) Loss: 919.1659 LL: -784.1547 KL: 135.0112 LL/KL: -5.8081
====> Epoch: 1890/5000 (38%) Loss: 1090.8901 LL: -956.9109 KL: 133.9793 LL/KL: -7.1422
====> Epoch: 1900/5000 (38%) Loss: 1087.7695 LL: -955.0302 KL: 132.7393 LL/KL: -7.1948
====> Epoch: 1910/5000 (38%) Loss: 924.7352 LL: -791.8412 KL: 132.8939 LL/KL: -5.9584
====> Epoch: 1920/5000 (38%) Loss: 1021.7333 LL: -889.7480 KL: 131.9854 LL/KL: -6.7413
====> Epoch: 1930/5000 (39%) Loss: 1017.7072 LL: -886.2141 KL: 131.4931 LL/KL: -6.7396
====> Epoch: 1940/5000 (39%) Loss: 926.9441 LL: -796.3915 KL: 130.5526 LL/KL: -6.1002
====> Epoch: 1950/5000 (39%) Loss: 1073.9729 LL: -944.9207 KL: 129.0522 LL/KL: -7.3220
====> Epoch: 1960/5000 (39%) Loss: 1322.2913 LL: -1192.1669 KL: 130.1244 LL/KL: -9.1617
====> Epoch: 1970/5000 (39%) Loss: 945.9066 LL: -816.6605 KL: 129.2461 LL/KL: -6.3186
====> Epoch: 1980/5000 (40%) Loss: 989.4670 LL: -861.0146 KL: 128.4525 LL/KL: -6.7030
====> Epoch: 1990/5000 (40%) Loss: 914.8405 LL: -787.3768 KL: 127.4637 LL/KL: -6.1773
====> Epoch: 2000/5000 (40%) Loss: 885.0105 LL: -758.5725 KL: 126.4380 LL/KL: -5.9996
====> Epoch: 2010/5000 (40%) Loss: 833.9244 LL: -707.5733 KL: 126.3511 LL/KL: -5.6001
====> Epoch: 2020/5000 (40%) Loss: 995.5771 LL: -870.4330 KL: 125.1441 LL/KL: -6.9554
====> Epoch: 2030/5000 (41%) Loss: 813.5052 LL: -689.0357 KL: 124.4695 LL/KL: -5.5358
====> Epoch: 2040/5000 (41%) Loss: 1232.0750 LL: -1106.8368 KL: 125.2381 LL/KL: -8.8379
====> Epoch: 2050/5000 (41%) Loss: 856.6201 LL: -733.6927 KL: 122.9274 LL/KL: -5.9685
====> Epoch: 2060/5000 (41%) Loss: 944.8660 LL: -821.5095 KL: 123.3565 LL/KL: -6.6596
====> Epoch: 2070/5000 (41%) Loss: 931.7560 LL: -809.6219 KL: 122.1340 LL/KL: -6.6290
====> Epoch: 2080/5000 (42%) Loss: 1089.9055 LL: -968.5006 KL: 121.4049 LL/KL: -7.9774
====> Epoch: 2090/5000 (42%) Loss: 819.7318 LL: -698.1631 KL: 121.5687 LL/KL: -5.7429
====> Epoch: 2100/5000 (42%) Loss: 808.8391 LL: -688.1251 KL: 120.7140 LL/KL: -5.7005
====> Epoch: 2110/5000 (42%) Loss: 903.3190 LL: -783.3751 KL: 119.9438 LL/KL: -6.5312
====> Epoch: 2120/5000 (42%) Loss: 927.3251 LL: -807.8618 KL: 119.4633 LL/KL: -6.7624
====> Epoch: 2130/5000 (43%) Loss: 1104.3967 LL: -985.5552 KL: 118.8415 LL/KL: -8.2930
====> Epoch: 2140/5000 (43%) Loss: 794.3965 LL: -676.0728 KL: 118.3237 LL/KL: -5.7138
====> Epoch: 2150/5000 (43%) Loss: 923.0366 LL: -805.5526 KL: 117.4840 LL/KL: -6.8567
====> Epoch: 2160/5000 (43%) Loss: 866.6819 LL: -749.9563 KL: 116.7256 LL/KL: -6.4250
====> Epoch: 2170/5000 (43%) Loss: 923.7598 LL: -806.1051 KL: 117.6547 LL/KL: -6.8514
====> Epoch: 2180/5000 (44%) Loss: 1001.1023 LL: -885.8831 KL: 115.2191 LL/KL: -7.6887
====> Epoch: 2190/5000 (44%) Loss: 991.2548 LL: -874.3283 KL: 116.9265 LL/KL: -7.4776
====> Epoch: 2200/5000 (44%) Loss: 822.8259 LL: -707.9806 KL: 114.8453 LL/KL: -6.1646
====> Epoch: 2210/5000 (44%) Loss: 904.2910 LL: -788.5288 KL: 115.7622 LL/KL: -6.8116
====> Epoch: 2220/5000 (44%) Loss: 939.7050 LL: -825.2687 KL: 114.4363 LL/KL: -7.2116
====> Epoch: 2230/5000 (45%) Loss: 804.5706 LL: -690.4047 KL: 114.1659 LL/KL: -6.0474
====> Epoch: 2240/5000 (45%) Loss: 834.5013 LL: -721.4212 KL: 113.0801 LL/KL: -6.3797
====> Epoch: 2250/5000 (45%) Loss: 970.1125 LL: -856.6547 KL: 113.4578 LL/KL: -7.5504
====> Epoch: 2260/5000 (45%) Loss: 941.7834 LL: -829.4613 KL: 112.3221 LL/KL: -7.3847
====> Epoch: 2270/5000 (45%) Loss: 827.0688 LL: -715.2425 KL: 111.8263 LL/KL: -6.3960
====> Epoch: 2280/5000 (46%) Loss: 992.4208 LL: -880.6038 KL: 111.8170 LL/KL: -7.8754
====> Epoch: 2290/5000 (46%) Loss: 837.1356 LL: -726.3115 KL: 110.8241 LL/KL: -6.5537
====> Epoch: 2300/5000 (46%) Loss: 806.1487 LL: -695.5837 KL: 110.5649 LL/KL: -6.2912
====> Epoch: 2310/5000 (46%) Loss: 818.8055 LL: -709.6201 KL: 109.1854 LL/KL: -6.4992
====> Epoch: 2320/5000 (46%) Loss: 916.8320 LL: -807.7577 KL: 109.0743 LL/KL: -7.4056
====> Epoch: 2330/5000 (47%) Loss: 857.3867 LL: -748.3130 KL: 109.0737 LL/KL: -6.8606
====> Epoch: 2340/5000 (47%) Loss: 796.6608 LL: -687.8863 KL: 108.7745 LL/KL: -6.3240
====> Epoch: 2350/5000 (47%) Loss: 1041.8469 LL: -933.2253 KL: 108.6217 LL/KL: -8.5915
====> Epoch: 2360/5000 (47%) Loss: 898.2067 LL: -790.9198 KL: 107.2868 LL/KL: -7.3720
====> Epoch: 2370/5000 (47%) Loss: 848.7167 LL: -741.1568 KL: 107.5599 LL/KL: -6.8906
====> Epoch: 2380/5000 (48%) Loss: 894.2069 LL: -787.5466 KL: 106.6603 LL/KL: -7.3837
====> Epoch: 2390/5000 (48%) Loss: 854.7635 LL: -748.6404 KL: 106.1232 LL/KL: -7.0544
====> Epoch: 2400/5000 (48%) Loss: 813.5554 LL: -707.4572 KL: 106.0982 LL/KL: -6.6679
====> Epoch: 2410/5000 (48%) Loss: 849.6256 LL: -743.7722 KL: 105.8535 LL/KL: -7.0264
====> Epoch: 2420/5000 (48%) Loss: 845.1296 LL: -740.3470 KL: 104.7825 LL/KL: -7.0656
====> Epoch: 2430/5000 (49%) Loss: 896.8544 LL: -792.3335 KL: 104.5209 LL/KL: -7.5806
====> Epoch: 2440/5000 (49%) Loss: 799.2703 LL: -694.8694 KL: 104.4009 LL/KL: -6.6558
====> Epoch: 2450/5000 (49%) Loss: 934.5477 LL: -831.3491 KL: 103.1985 LL/KL: -8.0558
====> Epoch: 2460/5000 (49%) Loss: 908.2848 LL: -803.9905 KL: 104.2943 LL/KL: -7.7089
====> Epoch: 2470/5000 (49%) Loss: 849.0633 LL: -746.2789 KL: 102.7844 LL/KL: -7.2606
====> Epoch: 2480/5000 (50%) Loss: 759.9329 LL: -657.3639 KL: 102.5690 LL/KL: -6.4090
====> Epoch: 2490/5000 (50%) Loss: 798.3906 LL: -695.7856 KL: 102.6049 LL/KL: -6.7812
====> Epoch: 2500/5000 (50%) Loss: 769.6586 LL: -667.6813 KL: 101.9772 LL/KL: -6.5474
====> Epoch: 2510/5000 (50%) Loss: 843.6807 LL: -742.0322 KL: 101.6485 LL/KL: -7.3000
====> Epoch: 2520/5000 (50%) Loss: 867.2152 LL: -765.6953 KL: 101.5199 LL/KL: -7.5423
====> Epoch: 2530/5000 (51%) Loss: 818.4354 LL: -717.7551 KL: 100.6803 LL/KL: -7.1291
====> Epoch: 2540/5000 (51%) Loss: 839.0244 LL: -738.4039 KL: 100.6205 LL/KL: -7.3385
====> Epoch: 2550/5000 (51%) Loss: 796.0190 LL: -695.0457 KL: 100.9733 LL/KL: -6.8835
====> Epoch: 2560/5000 (51%) Loss: 816.2598 LL: -716.5137 KL: 99.7460 LL/KL: -7.1834
====> Epoch: 2570/5000 (51%) Loss: 784.4588 LL: -684.5535 KL: 99.9053 LL/KL: -6.8520
====> Epoch: 2580/5000 (52%) Loss: 808.5016 LL: -709.4255 KL: 99.0760 LL/KL: -7.1604
====> Epoch: 2590/5000 (52%) Loss: 919.3453 LL: -820.2736 KL: 99.0717 LL/KL: -8.2796
====> Epoch: 2600/5000 (52%) Loss: 846.2645 LL: -747.6592 KL: 98.6054 LL/KL: -7.5823
====> Epoch: 2610/5000 (52%) Loss: 765.2324 LL: -667.5753 KL: 97.6572 LL/KL: -6.8359
====> Epoch: 2620/5000 (52%) Loss: 829.5279 LL: -731.4927 KL: 98.0351 LL/KL: -7.4615
====> Epoch: 2630/5000 (53%) Loss: 755.1743 LL: -657.5331 KL: 97.6411 LL/KL: -6.7342
====> Epoch: 2640/5000 (53%) Loss: 786.1245 LL: -689.2117 KL: 96.9128 LL/KL: -7.1117
====> Epoch: 2650/5000 (53%) Loss: 767.6805 LL: -671.1143 KL: 96.5663 LL/KL: -6.9498
====> Epoch: 2660/5000 (53%) Loss: 838.7776 LL: -742.1170 KL: 96.6606 LL/KL: -7.6776
====> Epoch: 2670/5000 (53%) Loss: 805.0795 LL: -709.1849 KL: 95.8946 LL/KL: -7.3955
====> Epoch: 2680/5000 (54%) Loss: 735.5726 LL: -639.8065 KL: 95.7661 LL/KL: -6.6809
====> Epoch: 2690/5000 (54%) Loss: 777.5686 LL: -681.7619 KL: 95.8067 LL/KL: -7.1160
====> Epoch: 2700/5000 (54%) Loss: 746.7385 LL: -651.6962 KL: 95.0423 LL/KL: -6.8569
====> Epoch: 2710/5000 (54%) Loss: 718.6770 LL: -623.8178 KL: 94.8592 LL/KL: -6.5763
====> Epoch: 2720/5000 (54%) Loss: 759.0612 LL: -665.6960 KL: 93.3651 LL/KL: -7.1300
====> Epoch: 2730/5000 (55%) Loss: 861.8386 LL: -767.6441 KL: 94.1945 LL/KL: -8.1496
====> Epoch: 2740/5000 (55%) Loss: 874.0099 LL: -780.4904 KL: 93.5195 LL/KL: -8.3457
====> Epoch: 2750/5000 (55%) Loss: 785.7666 LL: -692.4937 KL: 93.2729 LL/KL: -7.4244
====> Epoch: 2760/5000 (55%) Loss: 855.0970 LL: -762.0993 KL: 92.9977 LL/KL: -8.1948
====> Epoch: 2770/5000 (55%) Loss: 759.4047 LL: -666.8906 KL: 92.5142 LL/KL: -7.2085
====> Epoch: 2780/5000 (56%) Loss: 744.3246 LL: -652.2286 KL: 92.0960 LL/KL: -7.0820
====> Epoch: 2790/5000 (56%) Loss: 792.9471 LL: -700.4141 KL: 92.5330 LL/KL: -7.5693
====> Epoch: 2800/5000 (56%) Loss: 825.4376 LL: -734.3396 KL: 91.0980 LL/KL: -8.0610
====> Epoch: 2810/5000 (56%) Loss: 842.8924 LL: -751.2608 KL: 91.6316 LL/KL: -8.1987
====> Epoch: 2820/5000 (56%) Loss: 795.6002 LL: -704.7189 KL: 90.8813 LL/KL: -7.7543
====> Epoch: 2830/5000 (57%) Loss: 755.8378 LL: -665.3619 KL: 90.4760 LL/KL: -7.3540
====> Epoch: 2840/5000 (57%) Loss: 801.4414 LL: -710.7699 KL: 90.6715 LL/KL: -7.8390
====> Epoch: 2850/5000 (57%) Loss: 751.2559 LL: -661.1565 KL: 90.0994 LL/KL: -7.3381
====> Epoch: 2860/5000 (57%) Loss: 719.9642 LL: -630.4008 KL: 89.5634 LL/KL: -7.0386
====> Epoch: 2870/5000 (57%) Loss: 771.1097 LL: -681.4249 KL: 89.6847 LL/KL: -7.5980
====> Epoch: 2880/5000 (58%) Loss: 996.8088 LL: -907.6956 KL: 89.1132 LL/KL: -10.1859
====> Epoch: 2890/5000 (58%) Loss: 844.8672 LL: -755.9809 KL: 88.8863 LL/KL: -8.5050
====> Epoch: 2900/5000 (58%) Loss: 710.8585 LL: -621.3894 KL: 89.4691 LL/KL: -6.9453
====> Epoch: 2910/5000 (58%) Loss: 723.2809 LL: -635.7047 KL: 87.5763 LL/KL: -7.2589
====> Epoch: 2920/5000 (58%) Loss: 712.8298 LL: -624.1066 KL: 88.7232 LL/KL: -7.0343
====> Epoch: 2930/5000 (59%) Loss: 943.4076 LL: -855.8008 KL: 87.6068 LL/KL: -9.7687
====> Epoch: 2940/5000 (59%) Loss: 880.4826 LL: -792.7527 KL: 87.7299 LL/KL: -9.0363
====> Epoch: 2950/5000 (59%) Loss: 753.2102 LL: -665.9336 KL: 87.2766 LL/KL: -7.6302
====> Epoch: 2960/5000 (59%) Loss: 761.8583 LL: -675.3055 KL: 86.5528 LL/KL: -7.8022
====> Epoch: 2970/5000 (59%) Loss: 718.3149 LL: -631.8452 KL: 86.4697 LL/KL: -7.3071
====> Epoch: 2980/5000 (60%) Loss: 724.5120 LL: -638.4965 KL: 86.0155 LL/KL: -7.4230
====> Epoch: 2990/5000 (60%) Loss: 725.9197 LL: -639.5318 KL: 86.3879 LL/KL: -7.4030
====> Epoch: 3000/5000 (60%) Loss: 752.8986 LL: -666.8090 KL: 86.0895 LL/KL: -7.7455
====> Epoch: 3010/5000 (60%) Loss: 780.2025 LL: -695.3167 KL: 84.8858 LL/KL: -8.1912
====> Epoch: 3020/5000 (60%) Loss: 713.7156 LL: -628.0344 KL: 85.6813 LL/KL: -7.3299
====> Epoch: 3030/5000 (61%) Loss: 711.9158 LL: -627.5074 KL: 84.4085 LL/KL: -7.4342
====> Epoch: 3040/5000 (61%) Loss: 738.5993 LL: -653.7963 KL: 84.8030 LL/KL: -7.7096
====> Epoch: 3050/5000 (61%) Loss: 711.7902 LL: -627.6795 KL: 84.1107 LL/KL: -7.4625
====> Epoch: 3060/5000 (61%) Loss: 781.2863 LL: -697.0883 KL: 84.1980 LL/KL: -8.2792
====> Epoch: 3070/5000 (61%) Loss: 752.1160 LL: -668.0190 KL: 84.0971 LL/KL: -7.9434
====> Epoch: 3080/5000 (62%) Loss: 863.3893 LL: -779.8726 KL: 83.5168 LL/KL: -9.3379
====> Epoch: 3090/5000 (62%) Loss: 721.4332 LL: -637.9951 KL: 83.4381 LL/KL: -7.6463
====> Epoch: 3100/5000 (62%) Loss: 744.4059 LL: -661.2642 KL: 83.1417 LL/KL: -7.9535
====> Epoch: 3110/5000 (62%) Loss: 724.4175 LL: -641.5831 KL: 82.8344 LL/KL: -7.7454
====> Epoch: 3120/5000 (62%) Loss: 697.4312 LL: -615.3184 KL: 82.1128 LL/KL: -7.4936
====> Epoch: 3130/5000 (63%) Loss: 775.4492 LL: -693.1339 KL: 82.3153 LL/KL: -8.4205
====> Epoch: 3140/5000 (63%) Loss: 741.5649 LL: -659.5829 KL: 81.9821 LL/KL: -8.0455
====> Epoch: 3150/5000 (63%) Loss: 737.1166 LL: -654.8143 KL: 82.3023 LL/KL: -7.9562
====> Epoch: 3160/5000 (63%) Loss: 1023.9492 LL: -942.3915 KL: 81.5577 LL/KL: -11.5549
====> Epoch: 3170/5000 (63%) Loss: 728.7509 LL: -647.4678 KL: 81.2831 LL/KL: -7.9656
====> Epoch: 3180/5000 (64%) Loss: 735.9656 LL: -654.7540 KL: 81.2116 LL/KL: -8.0623
====> Epoch: 3190/5000 (64%) Loss: 754.7652 LL: -673.8146 KL: 80.9506 LL/KL: -8.3238
====> Epoch: 3200/5000 (64%) Loss: 774.4628 LL: -694.2424 KL: 80.2204 LL/KL: -8.6542
====> Epoch: 3210/5000 (64%) Loss: 687.0258 LL: -606.2477 KL: 80.7780 LL/KL: -7.5051
====> Epoch: 3220/5000 (64%) Loss: 740.8605 LL: -660.8254 KL: 80.0351 LL/KL: -8.2567
====> Epoch: 3230/5000 (65%) Loss: 684.2158 LL: -604.2495 KL: 79.9663 LL/KL: -7.5563
====> Epoch: 3240/5000 (65%) Loss: 773.5447 LL: -694.0251 KL: 79.5196 LL/KL: -8.7277
====> Epoch: 3250/5000 (65%) Loss: 695.9307 LL: -616.5854 KL: 79.3453 LL/KL: -7.7709
====> Epoch: 3260/5000 (65%) Loss: 681.2983 LL: -602.2036 KL: 79.0947 LL/KL: -7.6137
====> Epoch: 3270/5000 (65%) Loss: 687.6193 LL: -608.6228 KL: 78.9965 LL/KL: -7.7044
====> Epoch: 3280/5000 (66%) Loss: 682.1594 LL: -603.0143 KL: 79.1450 LL/KL: -7.6191
====> Epoch: 3290/5000 (66%) Loss: 670.1786 LL: -591.5975 KL: 78.5811 LL/KL: -7.5285
====> Epoch: 3300/5000 (66%) Loss: 655.3812 LL: -576.8384 KL: 78.5428 LL/KL: -7.3443
====> Epoch: 3310/5000 (66%) Loss: 693.5076 LL: -615.2990 KL: 78.2086 LL/KL: -7.8674
====> Epoch: 3320/5000 (66%) Loss: 688.3523 LL: -610.0354 KL: 78.3169 LL/KL: -7.7893
====> Epoch: 3330/5000 (67%) Loss: 722.6632 LL: -644.9954 KL: 77.6678 LL/KL: -8.3045
====> Epoch: 3340/5000 (67%) Loss: 687.7859 LL: -610.2338 KL: 77.5521 LL/KL: -7.8687
====> Epoch: 3350/5000 (67%) Loss: 715.3889 LL: -637.6036 KL: 77.7852 LL/KL: -8.1970
====> Epoch: 3360/5000 (67%) Loss: 702.4752 LL: -626.0345 KL: 76.4406 LL/KL: -8.1898
====> Epoch: 3370/5000 (67%) Loss: 678.0521 LL: -601.1630 KL: 76.8892 LL/KL: -7.8186
====> Epoch: 3380/5000 (68%) Loss: 653.9411 LL: -576.7960 KL: 77.1451 LL/KL: -7.4768
====> Epoch: 3390/5000 (68%) Loss: 671.2471 LL: -595.3273 KL: 75.9198 LL/KL: -7.8415
====> Epoch: 3400/5000 (68%) Loss: 659.8293 LL: -583.4724 KL: 76.3569 LL/KL: -7.6414
====> Epoch: 3410/5000 (68%) Loss: 667.2119 LL: -591.5807 KL: 75.6312 LL/KL: -7.8219
====> Epoch: 3420/5000 (68%) Loss: 664.8015 LL: -589.0865 KL: 75.7150 LL/KL: -7.7803
====> Epoch: 3430/5000 (69%) Loss: 649.1011 LL: -573.5612 KL: 75.5399 LL/KL: -7.5928
====> Epoch: 3440/5000 (69%) Loss: 703.9907 LL: -628.2757 KL: 75.7150 LL/KL: -8.2979
====> Epoch: 3450/5000 (69%) Loss: 786.0178 LL: -711.1376 KL: 74.8802 LL/KL: -9.4970
====> Epoch: 3460/5000 (69%) Loss: 717.5425 LL: -642.1110 KL: 75.4315 LL/KL: -8.5125
====> Epoch: 3470/5000 (69%) Loss: 674.7698 LL: -599.7651 KL: 75.0047 LL/KL: -7.9964
====> Epoch: 3480/5000 (70%) Loss: 670.2198 LL: -596.1570 KL: 74.0627 LL/KL: -8.0494
====> Epoch: 3490/5000 (70%) Loss: 723.9766 LL: -649.5585 KL: 74.4182 LL/KL: -8.7285
====> Epoch: 3500/5000 (70%) Loss: 653.7269 LL: -579.5652 KL: 74.1617 LL/KL: -7.8149
====> Epoch: 3510/5000 (70%) Loss: 704.2925 LL: -630.4770 KL: 73.8155 LL/KL: -8.5413
====> Epoch: 3520/5000 (70%) Loss: 663.5887 LL: -589.8456 KL: 73.7431 LL/KL: -7.9987
====> Epoch: 3530/5000 (71%) Loss: 811.7404 LL: -737.9393 KL: 73.8010 LL/KL: -9.9990
====> Epoch: 3540/5000 (71%) Loss: 641.0064 LL: -567.2764 KL: 73.7300 LL/KL: -7.6940
====> Epoch: 3550/5000 (71%) Loss: 736.5552 LL: -663.5878 KL: 72.9675 LL/KL: -9.0943
====> Epoch: 3560/5000 (71%) Loss: 651.6682 LL: -578.6369 KL: 73.0313 LL/KL: -7.9231
====> Epoch: 3570/5000 (71%) Loss: 672.8052 LL: -599.9281 KL: 72.8771 LL/KL: -8.2320
====> Epoch: 3580/5000 (72%) Loss: 662.6884 LL: -589.7836 KL: 72.9048 LL/KL: -8.0898
====> Epoch: 3590/5000 (72%) Loss: 686.2755 LL: -613.8436 KL: 72.4319 LL/KL: -8.4748
====> Epoch: 3600/5000 (72%) Loss: 702.3180 LL: -630.3293 KL: 71.9887 LL/KL: -8.7559
====> Epoch: 3610/5000 (72%) Loss: 672.2260 LL: -601.0071 KL: 71.2188 LL/KL: -8.4389
====> Epoch: 3620/5000 (72%) Loss: 643.2264 LL: -571.5139 KL: 71.7125 LL/KL: -7.9695
====> Epoch: 3630/5000 (73%) Loss: 835.7583 LL: -764.3203 KL: 71.4380 LL/KL: -10.6991
====> Epoch: 3640/5000 (73%) Loss: 649.7513 LL: -578.0388 KL: 71.7125 LL/KL: -8.0605
====> Epoch: 3650/5000 (73%) Loss: 660.5811 LL: -589.6147 KL: 70.9664 LL/KL: -8.3084
====> Epoch: 3660/5000 (73%) Loss: 680.0721 LL: -609.2243 KL: 70.8478 LL/KL: -8.5991
====> Epoch: 3670/5000 (73%) Loss: 642.3839 LL: -571.5682 KL: 70.8157 LL/KL: -8.0712
====> Epoch: 3680/5000 (74%) Loss: 703.7184 LL: -633.2766 KL: 70.4418 LL/KL: -8.9901
====> Epoch: 3690/5000 (74%) Loss: 645.6194 LL: -574.9556 KL: 70.6638 LL/KL: -8.1365
====> Epoch: 3700/5000 (74%) Loss: 619.0103 LL: -548.9799 KL: 70.0304 LL/KL: -7.8392
====> Epoch: 3710/5000 (74%) Loss: 674.1123 LL: -604.2333 KL: 69.8790 LL/KL: -8.6469
====> Epoch: 3720/5000 (74%) Loss: 637.6572 LL: -567.7590 KL: 69.8982 LL/KL: -8.1227
====> Epoch: 3730/5000 (75%) Loss: 652.8589 LL: -583.0005 KL: 69.8585 LL/KL: -8.3455
====> Epoch: 3740/5000 (75%) Loss: 620.5178 LL: -550.8807 KL: 69.6371 LL/KL: -7.9107
====> Epoch: 3750/5000 (75%) Loss: 642.7347 LL: -573.0463 KL: 69.6884 LL/KL: -8.2230
====> Epoch: 3760/5000 (75%) Loss: 618.5432 LL: -549.5834 KL: 68.9599 LL/KL: -7.9696
====> Epoch: 3770/5000 (75%) Loss: 652.9984 LL: -583.9424 KL: 69.0560 LL/KL: -8.4561
====> Epoch: 3780/5000 (76%) Loss: 641.5541 LL: -572.6702 KL: 68.8839 LL/KL: -8.3136
====> Epoch: 3790/5000 (76%) Loss: 693.9432 LL: -625.2040 KL: 68.7392 LL/KL: -9.0953
====> Epoch: 3800/5000 (76%) Loss: 622.7792 LL: -554.1230 KL: 68.6562 LL/KL: -8.0710
====> Epoch: 3810/5000 (76%) Loss: 616.5557 LL: -548.5389 KL: 68.0167 LL/KL: -8.0648
====> Epoch: 3820/5000 (76%) Loss: 626.2910 LL: -557.9468 KL: 68.3442 LL/KL: -8.1638
====> Epoch: 3830/5000 (77%) Loss: 708.0085 LL: -639.9651 KL: 68.0434 LL/KL: -9.4052
====> Epoch: 3840/5000 (77%) Loss: 637.8865 LL: -570.4841 KL: 67.4023 LL/KL: -8.4639
====> Epoch: 3850/5000 (77%) Loss: 655.0363 LL: -587.4722 KL: 67.5642 LL/KL: -8.6950
====> Epoch: 3860/5000 (77%) Loss: 711.0687 LL: -643.1337 KL: 67.9350 LL/KL: -9.4669
====> Epoch: 3870/5000 (77%) Loss: 758.9150 LL: -691.6280 KL: 67.2871 LL/KL: -10.2788
====> Epoch: 3880/5000 (78%) Loss: 643.4681 LL: -576.3708 KL: 67.0972 LL/KL: -8.5901
====> Epoch: 3890/5000 (78%) Loss: 669.4266 LL: -602.4955 KL: 66.9310 LL/KL: -9.0017
====> Epoch: 3900/5000 (78%) Loss: 630.6346 LL: -563.4401 KL: 67.1945 LL/KL: -8.3852
====> Epoch: 3910/5000 (78%) Loss: 622.6350 LL: -555.5162 KL: 67.1187 LL/KL: -8.2766
====> Epoch: 3920/5000 (78%) Loss: 663.4332 LL: -597.1276 KL: 66.3057 LL/KL: -9.0057
====> Epoch: 3930/5000 (79%) Loss: 609.6970 LL: -543.6302 KL: 66.0667 LL/KL: -8.2285
====> Epoch: 3940/5000 (79%) Loss: 607.8890 LL: -541.7928 KL: 66.0962 LL/KL: -8.1970
====> Epoch: 3950/5000 (79%) Loss: 720.4741 LL: -654.2028 KL: 66.2713 LL/KL: -9.8716
====> Epoch: 3960/5000 (79%) Loss: 630.8879 LL: -565.1665 KL: 65.7214 LL/KL: -8.5994
====> Epoch: 3970/5000 (79%) Loss: 617.7944 LL: -552.1035 KL: 65.6909 LL/KL: -8.4046
====> Epoch: 3980/5000 (80%) Loss: 620.5332 LL: -555.1282 KL: 65.4050 LL/KL: -8.4876
====> Epoch: 3990/5000 (80%) Loss: 638.1800 LL: -573.0204 KL: 65.1596 LL/KL: -8.7941
====> Epoch: 4000/5000 (80%) Loss: 600.0764 LL: -535.0825 KL: 64.9939 LL/KL: -8.2328
====> Epoch: 4010/5000 (80%) Loss: 605.8298 LL: -540.6980 KL: 65.1318 LL/KL: -8.3016
====> Epoch: 4020/5000 (80%) Loss: 639.2552 LL: -574.3159 KL: 64.9393 LL/KL: -8.8439
====> Epoch: 4030/5000 (81%) Loss: 612.0510 LL: -547.3312 KL: 64.7197 LL/KL: -8.4569
====> Epoch: 4040/5000 (81%) Loss: 622.6459 LL: -558.0066 KL: 64.6393 LL/KL: -8.6326
====> Epoch: 4050/5000 (81%) Loss: 593.4559 LL: -528.8130 KL: 64.6429 LL/KL: -8.1805
====> Epoch: 4060/5000 (81%) Loss: 652.0922 LL: -587.8282 KL: 64.2640 LL/KL: -9.1471
====> Epoch: 4070/5000 (81%) Loss: 616.7820 LL: -552.6750 KL: 64.1069 LL/KL: -8.6211
====> Epoch: 4080/5000 (82%) Loss: 614.1394 LL: -550.1802 KL: 63.9592 LL/KL: -8.6020
====> Epoch: 4090/5000 (82%) Loss: 593.4274 LL: -529.5789 KL: 63.8485 LL/KL: -8.2943
====> Epoch: 4100/5000 (82%) Loss: 614.1590 LL: -550.3714 KL: 63.7876 LL/KL: -8.6282
====> Epoch: 4110/5000 (82%) Loss: 698.9592 LL: -635.2255 KL: 63.7337 LL/KL: -9.9669
====> Epoch: 4120/5000 (82%) Loss: 597.7305 LL: -534.2497 KL: 63.4809 LL/KL: -8.4159
====> Epoch: 4130/5000 (83%) Loss: 625.5100 LL: -562.0518 KL: 63.4583 LL/KL: -8.8570
====> Epoch: 4140/5000 (83%) Loss: 600.7467 LL: -537.5049 KL: 63.2418 LL/KL: -8.4992
====> Epoch: 4150/5000 (83%) Loss: 587.2225 LL: -524.4268 KL: 62.7956 LL/KL: -8.3513
====> Epoch: 4160/5000 (83%) Loss: 582.7967 LL: -520.0049 KL: 62.7918 LL/KL: -8.2814
====> Epoch: 4170/5000 (83%) Loss: 574.0472 LL: -511.1793 KL: 62.8679 LL/KL: -8.1310
====> Epoch: 4180/5000 (84%) Loss: 578.9617 LL: -516.3944 KL: 62.5673 LL/KL: -8.2534
====> Epoch: 4190/5000 (84%) Loss: 577.7725 LL: -515.1024 KL: 62.6701 LL/KL: -8.2193
====> Epoch: 4200/5000 (84%) Loss: 601.2144 LL: -538.6915 KL: 62.5229 LL/KL: -8.6159
====> Epoch: 4210/5000 (84%) Loss: 668.2014 LL: -605.9390 KL: 62.2624 LL/KL: -9.7320
====> Epoch: 4220/5000 (84%) Loss: 599.4593 LL: -537.5534 KL: 61.9059 LL/KL: -8.6834
====> Epoch: 4230/5000 (85%) Loss: 615.6488 LL: -553.6359 KL: 62.0130 LL/KL: -8.9277
====> Epoch: 4240/5000 (85%) Loss: 556.5437 LL: -494.8093 KL: 61.7344 LL/KL: -8.0151
====> Epoch: 4250/5000 (85%) Loss: 582.6295 LL: -520.7747 KL: 61.8547 LL/KL: -8.4193
====> Epoch: 4260/5000 (85%) Loss: 583.5135 LL: -521.8832 KL: 61.6303 LL/KL: -8.4680
====> Epoch: 4270/5000 (85%) Loss: 568.6935 LL: -507.5081 KL: 61.1854 LL/KL: -8.2946
====> Epoch: 4280/5000 (86%) Loss: 612.7114 LL: -551.5659 KL: 61.1454 LL/KL: -9.0206
====> Epoch: 4290/5000 (86%) Loss: 575.8234 LL: -514.7766 KL: 61.0468 LL/KL: -8.4325
====> Epoch: 4300/5000 (86%) Loss: 567.5499 LL: -506.7109 KL: 60.8390 LL/KL: -8.3287
====> Epoch: 4310/5000 (86%) Loss: 612.3712 LL: -551.7848 KL: 60.5864 LL/KL: -9.1074
====> Epoch: 4320/5000 (86%) Loss: 572.0839 LL: -511.2029 KL: 60.8810 LL/KL: -8.3968
====> Epoch: 4330/5000 (87%) Loss: 560.6953 LL: -500.0361 KL: 60.6593 LL/KL: -8.2434
====> Epoch: 4340/5000 (87%) Loss: 590.0640 LL: -529.6385 KL: 60.4254 LL/KL: -8.7652
====> Epoch: 4350/5000 (87%) Loss: 561.7016 LL: -501.5230 KL: 60.1786 LL/KL: -8.3339
====> Epoch: 4360/5000 (87%) Loss: 647.8661 LL: -588.0090 KL: 59.8571 LL/KL: -9.8235
====> Epoch: 4370/5000 (87%) Loss: 566.7823 LL: -507.1593 KL: 59.6230 LL/KL: -8.5061
====> Epoch: 4380/5000 (88%) Loss: 572.4365 LL: -512.6395 KL: 59.7969 LL/KL: -8.5730
====> Epoch: 4390/5000 (88%) Loss: 585.4849 LL: -525.8849 KL: 59.5999 LL/KL: -8.8236
====> Epoch: 4400/5000 (88%) Loss: 586.9749 LL: -527.5110 KL: 59.4639 LL/KL: -8.8711
====> Epoch: 4410/5000 (88%) Loss: 598.1488 LL: -538.7944 KL: 59.3544 LL/KL: -9.0776
====> Epoch: 4420/5000 (88%) Loss: 579.3570 LL: -520.1516 KL: 59.2054 LL/KL: -8.7855
====> Epoch: 4430/5000 (89%) Loss: 567.6641 LL: -508.7092 KL: 58.9549 LL/KL: -8.6288
====> Epoch: 4440/5000 (89%) Loss: 570.8181 LL: -511.9452 KL: 58.8729 LL/KL: -8.6958
====> Epoch: 4450/5000 (89%) Loss: 563.7480 LL: -505.0131 KL: 58.7350 LL/KL: -8.5982
====> Epoch: 4460/5000 (89%) Loss: 557.3383 LL: -498.5407 KL: 58.7976 LL/KL: -8.4789
====> Epoch: 4470/5000 (89%) Loss: 551.9026 LL: -493.3624 KL: 58.5402 LL/KL: -8.4278
====> Epoch: 4480/5000 (90%) Loss: 580.9449 LL: -522.4132 KL: 58.5317 LL/KL: -8.9253
====> Epoch: 4490/5000 (90%) Loss: 553.7028 LL: -495.3785 KL: 58.3243 LL/KL: -8.4935
====> Epoch: 4500/5000 (90%) Loss: 587.8220 LL: -529.5482 KL: 58.2738 LL/KL: -9.0872
====> Epoch: 4510/5000 (90%) Loss: 561.2324 LL: -503.0823 KL: 58.1501 LL/KL: -8.6514
====> Epoch: 4520/5000 (90%) Loss: 536.5499 LL: -478.5396 KL: 58.0103 LL/KL: -8.2492
====> Epoch: 4530/5000 (91%) Loss: 586.3555 LL: -528.4722 KL: 57.8833 LL/KL: -9.1300
====> Epoch: 4540/5000 (91%) Loss: 571.4819 LL: -513.7173 KL: 57.7646 LL/KL: -8.8933
====> Epoch: 4550/5000 (91%) Loss: 577.7970 LL: -520.3825 KL: 57.4145 LL/KL: -9.0636
====> Epoch: 4560/5000 (91%) Loss: 542.3193 LL: -484.9071 KL: 57.4122 LL/KL: -8.4461
====> Epoch: 4570/5000 (91%) Loss: 532.9895 LL: -475.5977 KL: 57.3918 LL/KL: -8.2869
====> Epoch: 4580/5000 (92%) Loss: 551.8446 LL: -494.1960 KL: 57.6487 LL/KL: -8.5725
====> Epoch: 4590/5000 (92%) Loss: 550.6174 LL: -493.2253 KL: 57.3922 LL/KL: -8.5939
====> Epoch: 4600/5000 (92%) Loss: 547.4022 LL: -490.6758 KL: 56.7264 LL/KL: -8.6499
====> Epoch: 4610/5000 (92%) Loss: 559.5177 LL: -502.7200 KL: 56.7977 LL/KL: -8.8511
====> Epoch: 4620/5000 (92%) Loss: 546.1332 LL: -489.2809 KL: 56.8523 LL/KL: -8.6062
====> Epoch: 4630/5000 (93%) Loss: 557.4777 LL: -500.6660 KL: 56.8116 LL/KL: -8.8127
====> Epoch: 4640/5000 (93%) Loss: 550.1327 LL: -493.5694 KL: 56.5633 LL/KL: -8.7260
====> Epoch: 4650/5000 (93%) Loss: 534.5180 LL: -478.1115 KL: 56.4065 LL/KL: -8.4762
====> Epoch: 4660/5000 (93%) Loss: 523.9230 LL: -467.5148 KL: 56.4081 LL/KL: -8.2881
====> Epoch: 4670/5000 (93%) Loss: 531.8151 LL: -475.5070 KL: 56.3082 LL/KL: -8.4447
====> Epoch: 4680/5000 (94%) Loss: 539.2492 LL: -483.2094 KL: 56.0398 LL/KL: -8.6226
====> Epoch: 4690/5000 (94%) Loss: 584.3908 LL: -528.3885 KL: 56.0023 LL/KL: -9.4351
====> Epoch: 4700/5000 (94%) Loss: 542.7806 LL: -487.0355 KL: 55.7451 LL/KL: -8.7368
====> Epoch: 4710/5000 (94%) Loss: 543.7132 LL: -487.9923 KL: 55.7209 LL/KL: -8.7578
====> Epoch: 4720/5000 (94%) Loss: 582.5908 LL: -527.0165 KL: 55.5744 LL/KL: -9.4831
====> Epoch: 4730/5000 (95%) Loss: 571.3984 LL: -515.9402 KL: 55.4582 LL/KL: -9.3032
====> Epoch: 4740/5000 (95%) Loss: 528.4500 LL: -473.0062 KL: 55.4438 LL/KL: -8.5313
====> Epoch: 4750/5000 (95%) Loss: 544.4666 LL: -489.1317 KL: 55.3349 LL/KL: -8.8395
====> Epoch: 4760/5000 (95%) Loss: 556.6742 LL: -501.6004 KL: 55.0738 LL/KL: -9.1078
====> Epoch: 4770/5000 (95%) Loss: 533.8950 LL: -479.0010 KL: 54.8940 LL/KL: -8.7259
====> Epoch: 4780/5000 (96%) Loss: 562.5183 LL: -507.7845 KL: 54.7338 LL/KL: -9.2774
====> Epoch: 4790/5000 (96%) Loss: 516.1942 LL: -461.6894 KL: 54.5048 LL/KL: -8.4706
====> Epoch: 4800/5000 (96%) Loss: 559.5468 LL: -504.9055 KL: 54.6414 LL/KL: -9.2403
====> Epoch: 4810/5000 (96%) Loss: 536.0388 LL: -481.5584 KL: 54.4804 LL/KL: -8.8391
====> Epoch: 4820/5000 (96%) Loss: 532.1200 LL: -477.8788 KL: 54.2412 LL/KL: -8.8102
====> Epoch: 4830/5000 (97%) Loss: 536.3094 LL: -481.8954 KL: 54.4141 LL/KL: -8.8561
====> Epoch: 4840/5000 (97%) Loss: 514.1255 LL: -459.6886 KL: 54.4369 LL/KL: -8.4444
====> Epoch: 4850/5000 (97%) Loss: 530.4073 LL: -476.2966 KL: 54.1107 LL/KL: -8.8023
====> Epoch: 4860/5000 (97%) Loss: 524.8287 LL: -470.8121 KL: 54.0166 LL/KL: -8.7161
====> Epoch: 4870/5000 (97%) Loss: 527.7162 LL: -474.0122 KL: 53.7040 LL/KL: -8.8264
====> Epoch: 4880/5000 (98%) Loss: 514.6419 LL: -460.9665 KL: 53.6754 LL/KL: -8.5880
====> Epoch: 4890/5000 (98%) Loss: 579.9240 LL: -526.4152 KL: 53.5088 LL/KL: -9.8379
====> Epoch: 4900/5000 (98%) Loss: 515.9624 LL: -462.4415 KL: 53.5209 LL/KL: -8.6404
====> Epoch: 4910/5000 (98%) Loss: 531.2072 LL: -477.6583 KL: 53.5489 LL/KL: -8.9200
====> Epoch: 4920/5000 (98%) Loss: 547.7081 LL: -494.4285 KL: 53.2796 LL/KL: -9.2799
====> Epoch: 4930/5000 (99%) Loss: 522.3898 LL: -469.2688 KL: 53.1210 LL/KL: -8.8340
====> Epoch: 4940/5000 (99%) Loss: 511.6554 LL: -458.5463 KL: 53.1090 LL/KL: -8.6341
====> Epoch: 4950/5000 (99%) Loss: 516.1931 LL: -463.0934 KL: 53.0997 LL/KL: -8.7212
====> Epoch: 4960/5000 (99%) Loss: 525.2908 LL: -472.2451 KL: 53.0457 LL/KL: -8.9026
====> Epoch: 4970/5000 (99%) Loss: 524.9237 LL: -472.1770 KL: 52.7467 LL/KL: -8.9518
====> Epoch: 4980/5000 (100%) Loss: 536.8357 LL: -484.1406 KL: 52.6952 LL/KL: -9.1876
====> Epoch: 4990/5000 (100%) Loss: 503.3731 LL: -450.8439 KL: 52.5292 LL/KL: -8.5827
End fitting: 2021-01-08 18:02:35.806478
Elapsed: 0:00:30.538239
Deleting model.pt.running
Deleted: 2021-01-08 18:02:35.806616
Elapsed: 0:00:30.538765
## Plotting model convergence
plot_loss(model, skip=100)
skipping first 100 epochs where losses might be very high
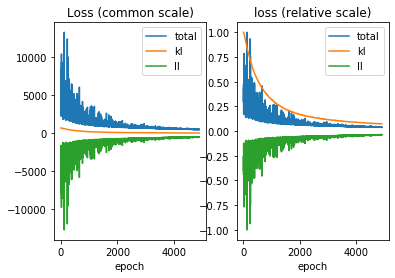
The plot above indicates that the model converged smoothly.
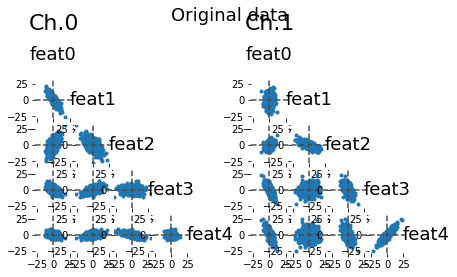
# We can plot the original data, dimension x dimension
lsplom(data, title = 'Original data')
# We can estimate the reconstructed data (decoding from the latent space)
x_hat = model.reconstruct(data)
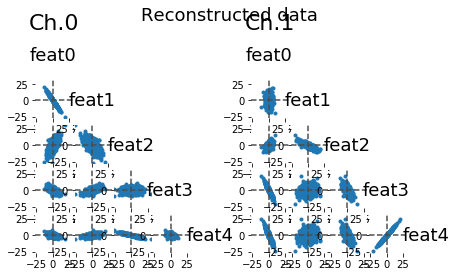
# Plotting the reconstructed data across dimensions
lsplom(x_hat, title = 'Reconstructed data')
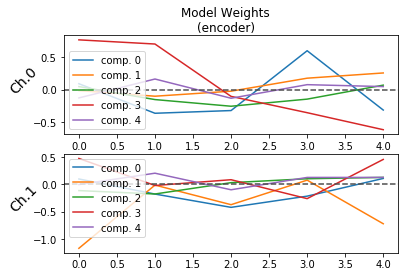
## Plotting the weights of the encoder
plot_weights(model, side = 'encoder')
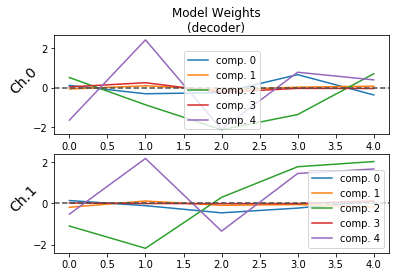
## Plotting the weights of the decoder
plot_weights(model, side = 'decoder')
# Inspecting model parameters
# Decoding parameters
weights_decoding_X = model.vae[0].W_out.weight.data
weights_decoding_Y = model.vae[1].W_out.weight.data
print(weights_decoding_X)
print(weights_decoding_Y)
tensor([[ 0.1148, -0.0684, 0.5098, 0.0365, -1.6451],
[-0.3095, 0.0943, -0.8667, 0.2497, 2.4173],
[-0.2510, -0.1134, -2.1274, -0.2352, -2.1068],
[ 0.6572, 0.0243, -1.3619, -0.0370, 0.7790],
[-0.3694, 0.0762, 0.7014, -0.0429, 0.3934]])
tensor([[ 0.1395, -0.1859, -1.0957, 0.0222, -0.5188],
[-0.1095, 0.1167, -2.1759, -0.0054, 2.1793],
[-0.4565, -0.0929, 0.2947, -0.0118, -1.3441],
[-0.2269, -0.0548, 1.7775, -0.0096, 1.4515],
[ 0.1131, -0.1738, 2.0298, 0.1213, 1.6703]])
# Encoding parameters
weights_encoding_X = model.vae[0].W_mu.weight.data
weights_encoding_Y = model.vae[1].W_mu.weight.data
print(weights_encoding_X)
print(weights_encoding_Y)
tensor([[ 0.0909, -0.3644, -0.3227, 0.5998, -0.3149],
[-0.0150, -0.1016, -0.0240, 0.1764, 0.2570],
[ 0.0469, -0.1533, -0.2561, -0.1465, 0.0691],
[ 0.7675, 0.7032, -0.1042, -0.3557, -0.6180],
[-0.1278, 0.1636, -0.1328, 0.0766, 0.0469]])
tensor([[ 0.1005, -0.1762, -0.4199, -0.2145, 0.1101],
[-1.1709, -0.0119, -0.3710, 0.0791, -0.7206],
[-0.1125, -0.1749, 0.0331, 0.1045, 0.1293],
[ 0.4766, -0.0190, 0.0869, -0.2600, 0.4588],
[-0.0017, 0.2063, -0.0976, 0.1288, 0.1290]])
# Here we compute the encoding and plot the latent dimensions against our original ground truth for the syntetic data
encoding = model.encode(data)
# Remember: encodings are distributions
print(f'Encoding distribution q for Channel 0: {encoding[0]}')
# with the method "loc" we extract the mean of the distributions
encoding_x = encoding[0].loc.data.numpy()
encoding_y = encoding[1].loc.data.numpy()
Encoding distribution q for Channel 0: Normal(loc: torch.Size([500, 5]), scale: torch.Size([500, 5]))
We note that the estimated encoding is correlated with the original latent dimensions. There seems to be however some redundancy. This motivates the use of a sparse model.
plt.figure(figsize=(12, 12))
for idx,k in enumerate(range(n_components)):
plt.subplot(n_components,2,2*idx+1)
plt.scatter(encoding_x[:,k], latents[:,0])
plt.xlabel(f'mcvae dim {k}')
plt.ylabel('ground truth 0')
plt.subplot(n_components,2,2*idx+2)
plt.scatter(encoding_x[:,k], latents[:,1])
plt.xlabel(f'mcvae dim {k}')
plt.ylabel('ground truth 1')
plt.tight_layout()
plt.show()
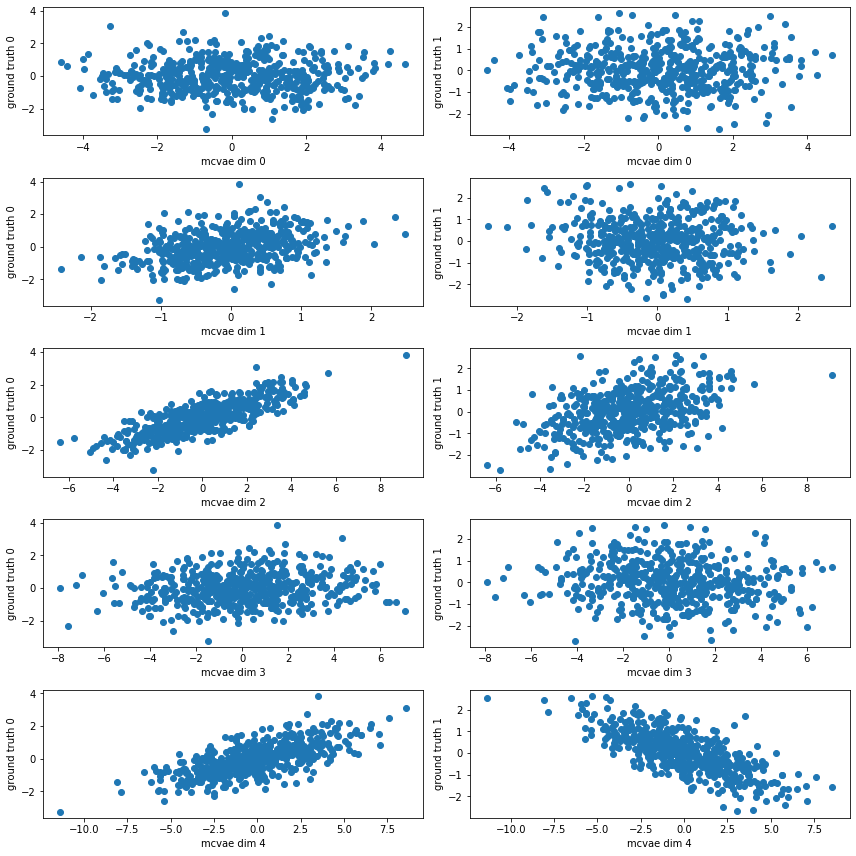
# Initialize sparse mcvae
model_sparse1 = Mcvae(sparse=True, **init_dict)
model_sparse1.to(DEVICE)
print(model_sparse1)
Mcvae(
(vae): ModuleList(
(0): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 5]))
(log_alpha): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=5, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=5, bias=True)
)
(1): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 5]))
(log_alpha): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=5, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=5, bias=True)
)
)
)
# Optimize
model_sparse1.optimizer = torch.optim.Adam(model_sparse1.parameters(), lr=adam_lr)
load_or_fit(model=model_sparse1, data=data, epochs=n_epochs, ptfile='model_sparse1.pt', force_fit=FORCE_REFIT)
Loading model_sparse1.pt
The sparse model estimates a probability of redundancy associated to each dimension. This means that we can retain only the dimensions with low probability of redundancy. In this case the model correctly identifies only 2 meaningful latent dimensions.
print('Probability of redundancy: ', model_sparse1.dropout.data)
plot_dropout(model_sparse1, sort=False)
Probability of redundancy: tensor([[0.5597, 0.5693, 0.0177, 0.0296, 0.5730]])
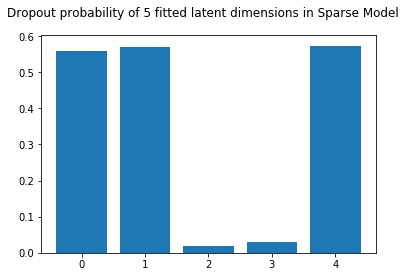
# We fix a redundancy threshold
dropout_threshold = 0.20
# We plot the remaining latent dimensions
keep = (model_sparse1.dropout.squeeze() < dropout_threshold).tolist()
kept_comps = [i for i, kept in enumerate(keep) if kept]
print(f'kept components: {kept_comps}')
plot_latent_space(model_sparse1, data=data, comp=kept_comps);
kept components: [2, 3]

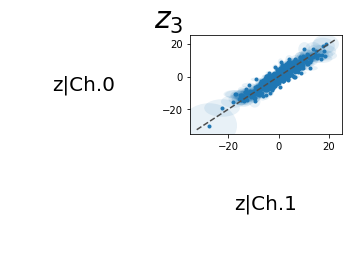
# We repeate the same exercise with the synthetic data with redundant dimensions
data_sparse = [X_ext, Y_ext]
data_sparse = [torch.Tensor(_) for _ in data_sparse]
init_dict = {
'data': data_sparse,
'lat_dim': n_components + 3,
}
model_sparse = Mcvae(sparse=True, **init_dict)
model_sparse.to(DEVICE)
print(model_sparse)
Mcvae(
(vae): ModuleList(
(0): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 8]))
(log_alpha): Parameter(shape=torch.Size([1, 8]))
(W_mu): Linear(in_features=8, out_features=8, bias=True)
(W_out): Linear(in_features=8, out_features=8, bias=True)
)
(1): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 8]))
(log_alpha): Parameter(shape=torch.Size([1, 8]))
(W_mu): Linear(in_features=8, out_features=8, bias=True)
(W_out): Linear(in_features=8, out_features=8, bias=True)
)
)
)
# Fit (or load model if existing)
model_sparse.optimizer = torch.optim.Adam(model_sparse.parameters(), lr=adam_lr)
load_or_fit(model=model_sparse, data=data_sparse, epochs=n_epochs, ptfile='model_sparse.pt', force_fit=FORCE_REFIT)
Loading model_sparse.pt
We see that the model recognises again only two meaningful latent dimensions
print('Probability of redundancy: ', model_sparse.dropout.data)
indices = np.where(model_sparse.dropout.data.numpy().flatten() < dropout_threshold)[0]
non_redundant_comps = indices.tolist()
print(f'Non-redundant components: {non_redundant_comps}')
plot_dropout(model_sparse, sort=False)
Probability of redundancy: tensor([[0.7038, 0.7494, 0.7669, 0.0166, 0.8116, 0.0525, 0.6920, 0.7680]])
Non-redundant components: [3, 5]
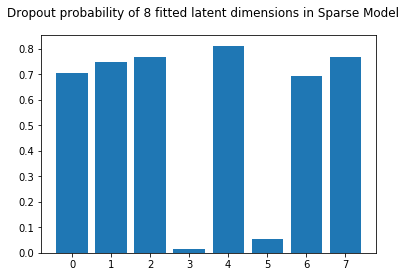
x_hat = model_sparse.reconstruct(data_sparse, dropout_threshold=dropout_threshold)
lsplom(x_hat, title = 'Reconstructed data')
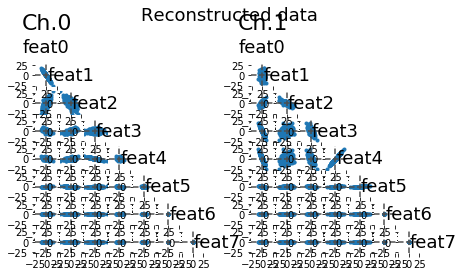
## Plotting the weights of the decoder
plt.figure(figsize=(12, 8))
plot_weights(model_sparse, side = 'decoder')
<Figure size 864x576 with 0 Axes>
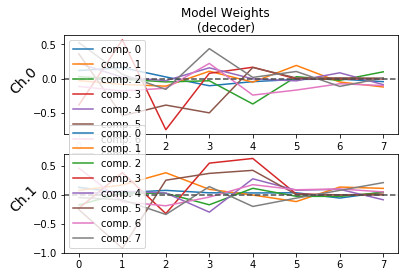
plt.figure(figsize=(12, 8))
plot_weights(model_sparse, side = 'encoder')
<Figure size 864x576 with 0 Axes>
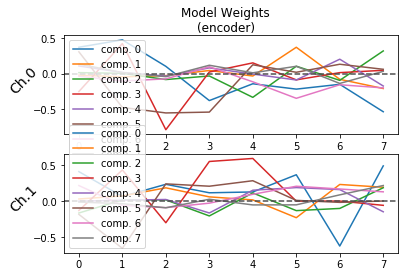
# PLotting estimated encoding vs ground truth
encoding = model_sparse.encode(data_sparse)
encoding_x = encoding[0].loc.detach().numpy()
encoding_y = encoding[1].loc.detach().numpy()
plt.figure(figsize=(12, 12))
for idx,k in enumerate(indices):
plt.subplot(len(indices),2,2*idx+1)
plt.scatter(encoding_x[:,k], latents[:,0])
plt.xlabel(str('mcvae dim ') + str(k))
plt.ylabel('ground truth 0')
plt.subplot(len(indices),2,2*idx+2)
plt.scatter(encoding_x[:,k], latents[:,1])
plt.xlabel(str('mcvae dim ') + str(k))
plt.ylabel('ground truth 1')
plt.show()
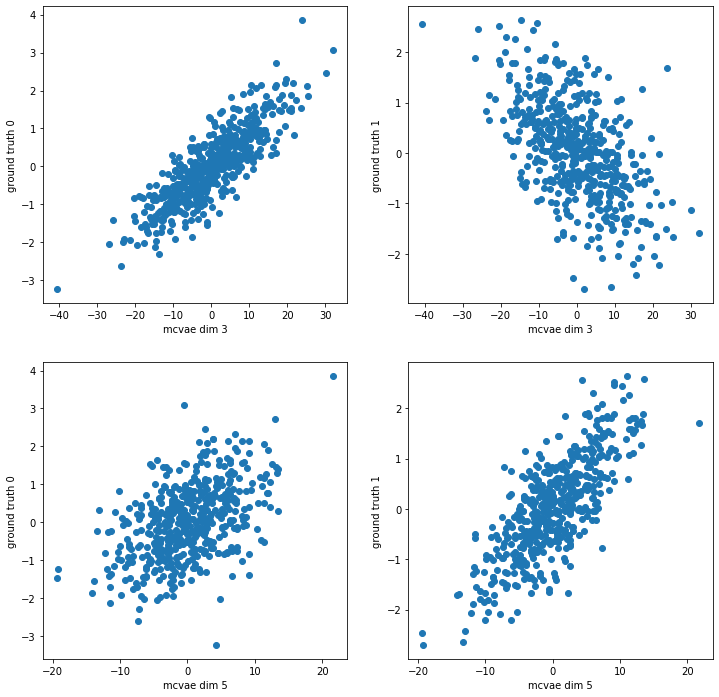
plot_latent_space(model_sparse, data_sparse, comp=non_redundant_comps);


Increasing the number of channels¶
In this section we explore the use of the model on data with multiple modalities (or channels)
# generating a new modality Z
# This modality has meaningful as well as redundant dimensions
size_z = 10
size_z_redundant = 4
np.random.seed(37)
Z_redundant = np.random.randn(n, size_z_redundant) # pure noise
transform_z = np.random.randint(-8, 8, size=(2, size_z))
Z = latents.dot(transform_z) + 2*np.random.normal(size=(n, size_z))
Z = np.hstack([Z, Z_redundant])
print(X_ext.shape,Y_ext.shape, Z.shape)
(500, 8) (500, 8) (500, 14)
# Initialize the model
data_multi = [X_ext, Y_ext, Z]
data_multi = [torch.Tensor(_) for _ in data_multi]
init_dict = {
'data': data_multi, # [X, Y, Z]
'lat_dim': n_components + 3,
}
model_multi = Mcvae(sparse=True, **init_dict)
model_multi.to(DEVICE)
print(model_multi)
Mcvae(
(vae): ModuleList(
(0): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 8]))
(log_alpha): Parameter(shape=torch.Size([1, 8]))
(W_mu): Linear(in_features=8, out_features=8, bias=True)
(W_out): Linear(in_features=8, out_features=8, bias=True)
)
(1): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 8]))
(log_alpha): Parameter(shape=torch.Size([1, 8]))
(W_mu): Linear(in_features=8, out_features=8, bias=True)
(W_out): Linear(in_features=8, out_features=8, bias=True)
)
(2): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 14]))
(log_alpha): Parameter(shape=torch.Size([1, 8]))
(W_mu): Linear(in_features=14, out_features=8, bias=True)
(W_out): Linear(in_features=8, out_features=14, bias=True)
)
)
)
# Fit (or load)
model_multi.optimizer = torch.optim.Adam(model_multi.parameters(), lr=adam_lr)
load_or_fit(model=model_multi, data=data_multi, epochs=n_epochs, ptfile='model_multi.pt', force_fit=FORCE_REFIT)
Loading model_multi.pt
print('Probability of redundancy: ', model_multi.dropout.data.numpy())
indices = np.where(model_multi.dropout.data.numpy().flatten() < dropout_threshold)[0]
print('Non-redundant components: ', indices)
plot_dropout(model_multi, sort=False)
encoding = model_multi.encode(data_multi)
encoding_x = encoding[0].loc.detach().numpy()
encoding_y = encoding[1].loc.detach().numpy()
encoding_z = encoding[2].loc.detach().numpy()
plt.figure(figsize=(12, 12))
for idx,k in enumerate(indices):
plt.subplot(len(indices),2,2*idx+1)
plt.scatter(encoding_z[:,k], latents[:,0])
plt.xlabel(str('mcvae dim ') + str(k))
plt.ylabel('ground truth 0')
plt.subplot(len(indices),2,2*idx+2)
plt.scatter(encoding_z[:,k], latents[:,1])
plt.xlabel(str('mcvae dim ') + str(k))
plt.ylabel('ground truth 1')
plt.show()
Probability of redundancy: [[0.03285351 0.39449245 0.00762853 0.60119134 0.59263474 0.6564989
0.25333416 0.3858575 ]]
Non-redundant components: [0 2]
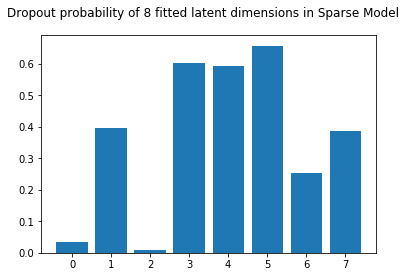
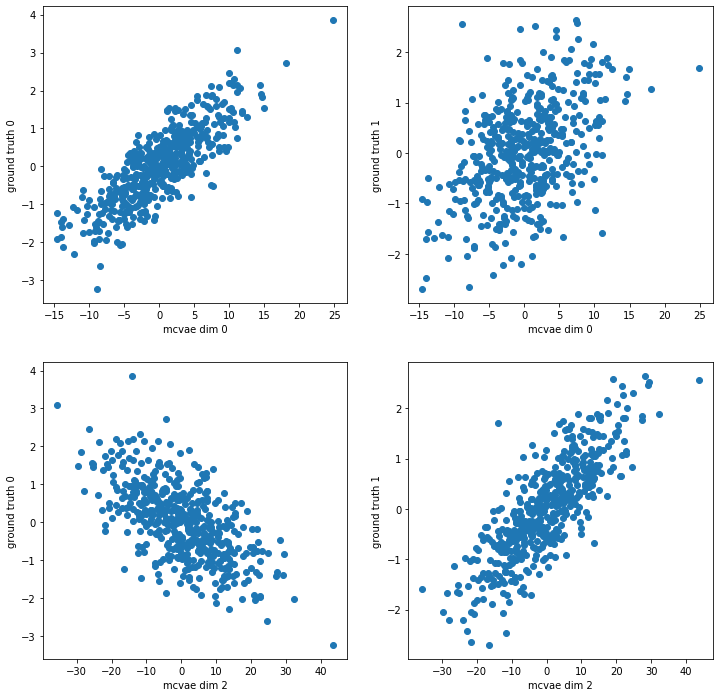
The multi-channel variational autoencoder allows to predict each channel from any other.
# We compute the reconstruction of the data from the encoding
z = [_.sample() for _ in encoding] # sample the encoding distributions
p = model_multi.decode(z) # compute the decoding distributions
# This variable has several dimensions over two indices:
# the first index indicates the modality to decode(0:x, 1:y, 3:z, ...)
# the second index indicates the modality from which the encoding is done (0:x, 1:y, 3:z, ...)
# p[x][z]: p(x|z)
decoding_x_from_x = p[0][0].loc.data.numpy()
decoding_x_from_y = p[0][1].loc.data.numpy()
decoding_x_from_z = p[0][2].loc.data.numpy()
plt.figure(figsize=(18, 10))
plt.subplot(2,3,1)
plt.scatter(X_ext[:,0], decoding_x_from_x[:,0])
plt.title('decoding X from X')
plt.xlabel('X0')
plt.ylabel('X0 from latent X')
plt.subplot(2,3,2)
plt.scatter(X_ext[:,0], decoding_x_from_y[:,0])
plt.title('decoding X from Y')
plt.ylabel('X0 from latent Y')
plt.xlabel('X0')
plt.subplot(2,3,3)
plt.scatter(X_ext[:,0], decoding_x_from_z[:,0])
plt.title('decoding X from Z')
plt.xlabel('X0')
plt.ylabel('X0 from latent Z')
plt.subplot(2,3,4)
plt.scatter(decoding_x_from_x[:,0], decoding_x_from_y[:,0])
plt.title('decoding X vs decoding Y')
plt.xlabel('X0 from latent X')
plt.ylabel('X0 from latent Y')
plt.subplot(2,3,5)
plt.scatter(decoding_x_from_x[:,0], decoding_x_from_z[:,0])
plt.title('decoding Y vs decoding Z')
plt.xlabel('X0 from latent X')
plt.ylabel('X0 from latent Z')
plt.subplot(2,3,6)
plt.scatter(decoding_x_from_y[:,0], decoding_x_from_z[:,0])
plt.title('decoding Y vs decoding Z')
plt.xlabel('X0 from latent Y')
plt.ylabel('X0 from latent Z')
plt.tight_layout()
plt.show()
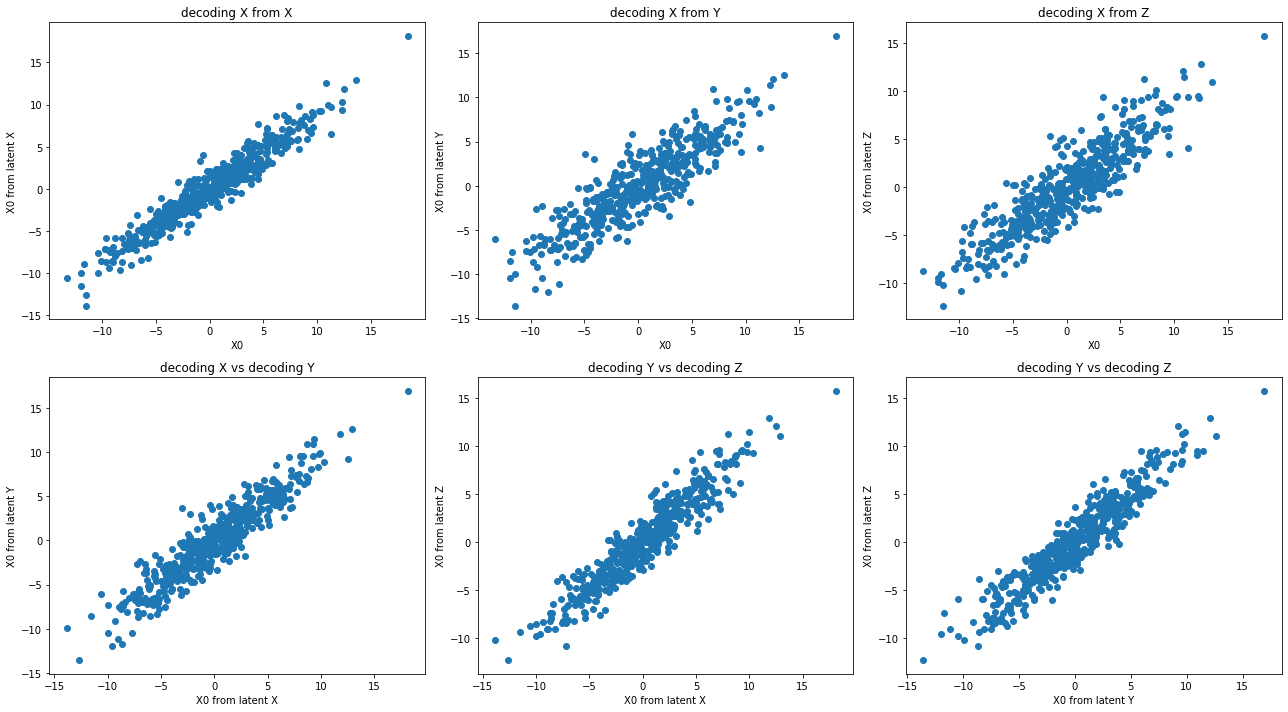
Application to (pseudo-) neurological data¶
We are going to load volumetric and cognitive data for a synthetic sample generated from the ADNI dataset. The exercise consists in applying the methods seen so far to understand the relationship between this kind of variables.
import pandas as pd
adni = pd.read_csv('https://marcolorenzi.github.io/material/pseudo_adni.csv')
brain_volume_cols = ['WholeBrain.bl', 'Ventricles.bl', 'Hippocampus.bl', 'MidTemp.bl', 'Entorhinal.bl']
cognition_cols = ['CDRSB.bl', 'ADAS11.bl', 'MMSE.bl', 'RAVLT.immediate.bl', 'RAVLT.learning.bl', 'RAVLT.forgetting.bl', 'FAQ.bl']
adni[brain_volume_cols]
| WholeBrain.bl | Ventricles.bl | Hippocampus.bl | MidTemp.bl | Entorhinal.bl | |
|---|---|---|---|---|---|
| 0 | 0.684331 | 0.012699 | 0.003786 | 0.012678 | 0.002214 |
| 1 | 0.735892 | 0.012803 | 0.004866 | 0.015071 | 0.003041 |
| 2 | 0.738731 | 0.030492 | 0.004300 | 0.012419 | 0.002316 |
| 3 | 0.696179 | 0.032797 | 0.004720 | 0.012312 | 0.002593 |
| 4 | 0.841806 | 0.004030 | 0.006820 | 0.016948 | 0.002896 |
| ... | ... | ... | ... | ... | ... |
| 995 | 0.767153 | 0.011417 | 0.005209 | 0.012879 | 0.002208 |
| 996 | 0.695168 | 0.011908 | 0.004641 | 0.012534 | 0.002197 |
| 997 | 0.628691 | 0.041537 | 0.003478 | 0.010870 | 0.001939 |
| 998 | 0.714763 | 0.020461 | 0.004713 | 0.013989 | 0.001981 |
| 999 | 0.691858 | 0.030349 | 0.004237 | 0.011439 | 0.002419 |
1000 rows × 5 columns
volumes_value = adni[brain_volume_cols].values
# Standardization of volumetric measures
volumes_value = (volumes_value - volumes_value.mean(0)) / volumes_value.std(0)
adni[cognition_cols]
| CDRSB.bl | ADAS11.bl | MMSE.bl | RAVLT.immediate.bl | RAVLT.learning.bl | RAVLT.forgetting.bl | FAQ.bl | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 8 | 27.0 | 23.739439 | 4.0 | 5.821573 | 3 |
| 1 | 0 | 0 | 30.0 | 64.933800 | 9.0 | 4.001653 | 0 |
| 2 | 0 | 8 | 24.0 | 36.987722 | 3.0 | 6.876316 | 0 |
| 3 | 0 | 3 | 29.0 | 50.314425 | 5.0 | 4.733481 | 3 |
| 4 | 0 | 0 | 30.0 | 57.217830 | 9.0 | 7.225401 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 995 | 1 | 2 | 29.0 | 61.896022 | 8.0 | 1.663102 | 0 |
| 996 | 0 | 1 | 29.0 | 62.083170 | 8.0 | 5.241477 | 1 |
| 997 | 3 | 14 | 24.0 | 22.289059 | 2.0 | 5.437600 | 7 |
| 998 | 0 | 13 | 26.0 | 31.650504 | 2.0 | 1.669603 | 4 |
| 999 | 0 | 15 | 28.0 | 29.089863 | 3.0 | 7.703384 | 4 |
1000 rows × 7 columns
cognition_value = adni[cognition_cols].values
# Standardization of cognitive measures
cognition_value = (cognition_value - cognition_value.mean(0)) / cognition_value.std(0)
Exercise (a). Use PLS to model the relationship between cognitive variables and brain volumes. How many latent components are needed?
Exercise (b). Explore the PLS model weights to interpret the relationship between the variables identified by the model.
McVAE¶
In this last application we apply the multichannel autoencoder to the pseudo-ADNI data, for jointly modeling different modalities across individuals. We focus on the joint analysis of:
brain volumes;
sociodemographic information (e.g. age, sex, scholarity);
cognition;
apoe genotype;
fluid biomarkers (abeta and tay concentrations in the CSF).
We first import and standardize the different data modalities.
adni = pd.read_csv('https://marcolorenzi.github.io/material/pseudo_adni.csv')
normalize = lambda _: (_ - _.mean(0))/_.std(0)
volume_cols = ['WholeBrain.bl', 'Ventricles.bl', 'Hippocampus.bl', 'MidTemp.bl', 'Entorhinal.bl']
volumes_value = adni[volume_cols].values
volumes_value = normalize(volumes_value)
demog_cols = ['SEX', 'AGE', 'PTEDUCAT']
demog_value = adni[demog_cols].values
demog_value = normalize(demog_value)
cognition_cols = ['CDRSB.bl', 'ADAS11.bl', 'MMSE.bl', 'RAVLT.immediate.bl', 'RAVLT.learning.bl', 'RAVLT.forgetting.bl', 'FAQ.bl']
cognition_value = adni[cognition_cols].values
cognition_value = normalize(cognition_value)
apoe_cols = ['APOE4']
apoe_value = adni[apoe_cols].values
apoe_value = normalize(apoe_value)
fluid_cols = ['ABETA.MEDIAN.bl', 'PTAU.MEDIAN.bl', 'TAU.MEDIAN.bl']
fluid_value = adni[fluid_cols].values
fluid_value = normalize(fluid_value)
# Creating a list with multimodal data
data_adni = [volumes_value, demog_value, cognition_value, apoe_value, fluid_value]
adni_cols = [volume_cols, demog_cols, cognition_cols, apoe_cols, fluid_cols]
# Transform as a pytorch Tensor for compatibility
data_adni = [torch.Tensor(_) for _ in data_adni]
print(f'We have {len(data_adni)} channels in total as an input for the model')
We have 5 channels in total as an input for the model
##############################################
## FIT a Sparse Mcvae with Pseudo-Adni data ##
##############################################
# create an instance of the model
model_adni = Mcvae(data = data_adni, lat_dim = 5, sparse=True)
model_adni.to(DEVICE)
print(model_adni)
# set up the optimizer
adam_lr = 1e-2
n_epochs = 6000
model_adni.optimizer = torch.optim.Adam(model_adni.parameters(), lr=1e-2)
# fit
load_or_fit(model=model_adni, data=data_adni, epochs=6000, ptfile='model_adni.pt', force_fit=FORCE_REFIT)
Mcvae(
(vae): ModuleList(
(0): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 5]))
(log_alpha): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=5, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=5, bias=True)
)
(1): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 3]))
(log_alpha): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=3, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=3, bias=True)
)
(2): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 7]))
(log_alpha): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=7, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=7, bias=True)
)
(3): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 1]))
(log_alpha): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=1, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=1, bias=True)
)
(4): VAE(
(W_out_logvar): Parameter(shape=torch.Size([1, 3]))
(log_alpha): Parameter(shape=torch.Size([1, 5]))
(W_mu): Linear(in_features=3, out_features=5, bias=True)
(W_out): Linear(in_features=5, out_features=3, bias=True)
)
)
)
Loading model_adni.pt
# Check convergence
plot_loss(model_adni)
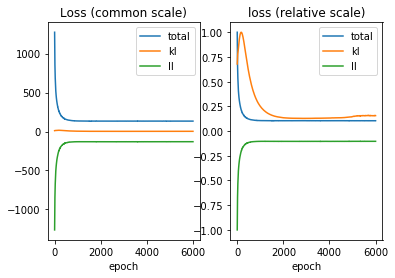
The model identified only a significant dimension, that we are going to store and analyze:
# Identify the most significant latent dimension
plot_dropout(model_adni)
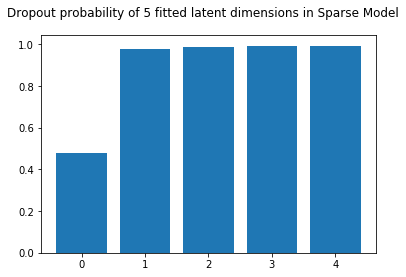
kept_dim = 0
The weights give us a nice way to interpret how the different modalities interact together.
# Plot the decoding weights (the generative parameters)
# associated to the non-redundant dimension latent dimension
# Store the weights (use the practical "dot" notation model.vae[i].W_out.weight)
decoding_weights = [vae.W_out.weight.data[:, kept_dim] for vae in model_adni]
# Plot
plt.figure(figsize=(12, 12))
for i in range(len(data_adni)):
plt.subplot(5,1,i+1)
plt.bar(np.arange(len(decoding_weights[i])), decoding_weights[i], tick_label = adni_cols[i])
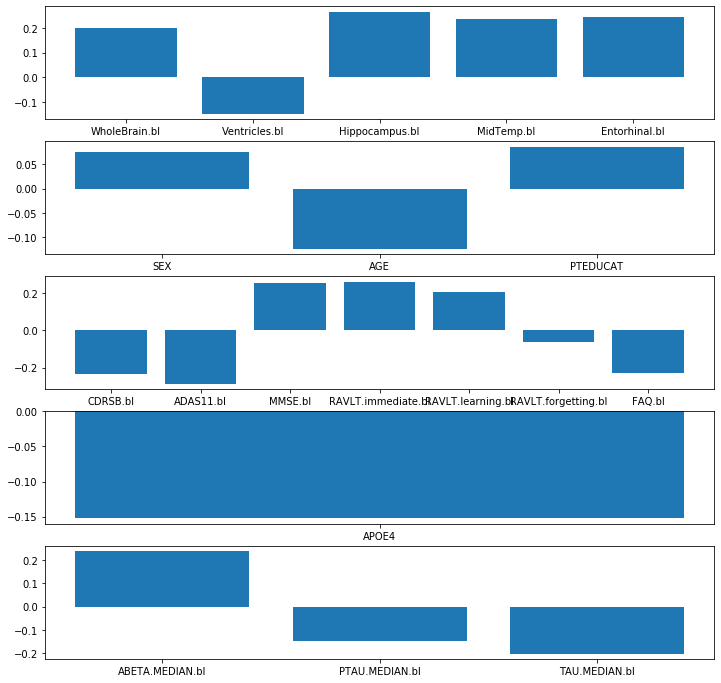
Once the model is learnt we can use it for prediction. For example we can predict brain volumes from the cognitive data:
# Predict volumes (channel 0) from cognition (channel 2)
# Solution 1
# Encode everything
q = model_adni.encode(data_adni)
# Take the mean of every encoded distribution q
z = [qi.loc for qi in q]
# Decode all
p = model_adni.decode(z)
# Extract what you need: p(x|z) or p[x][z] or p[decoder output channel][encoder input chanenl]
decoding_volume_from_cognition = p[0][2].loc.data.numpy()
# Solution 2
# Encode the cognition (ch 2)
q2 = model_adni.vae[2].encode(data_adni[2])
# Take the mean of q (location in pytorch jargon)
z2 = q2.loc
# Decode through the brain volumes decoder (ch 0)
p0 = model_adni.vae[0].decode(z2)
# Take the mean
decoding_volume_from_cognition = p0.loc.data.numpy()
# Plot the predicted volumes against the true ones.
# Create one plot per volumetric feature
plt.figure(figsize=(12, 28))
for i in range(len(volume_cols)):
plt.subplot(5,1,i+1)
plt.scatter(decoding_volume_from_cognition[:,i], volumes_value[:,i])
plt.title('reconstruction ' + volume_cols[i])
plt.xlabel('predicted')
plt.ylabel('target')
plt.show()
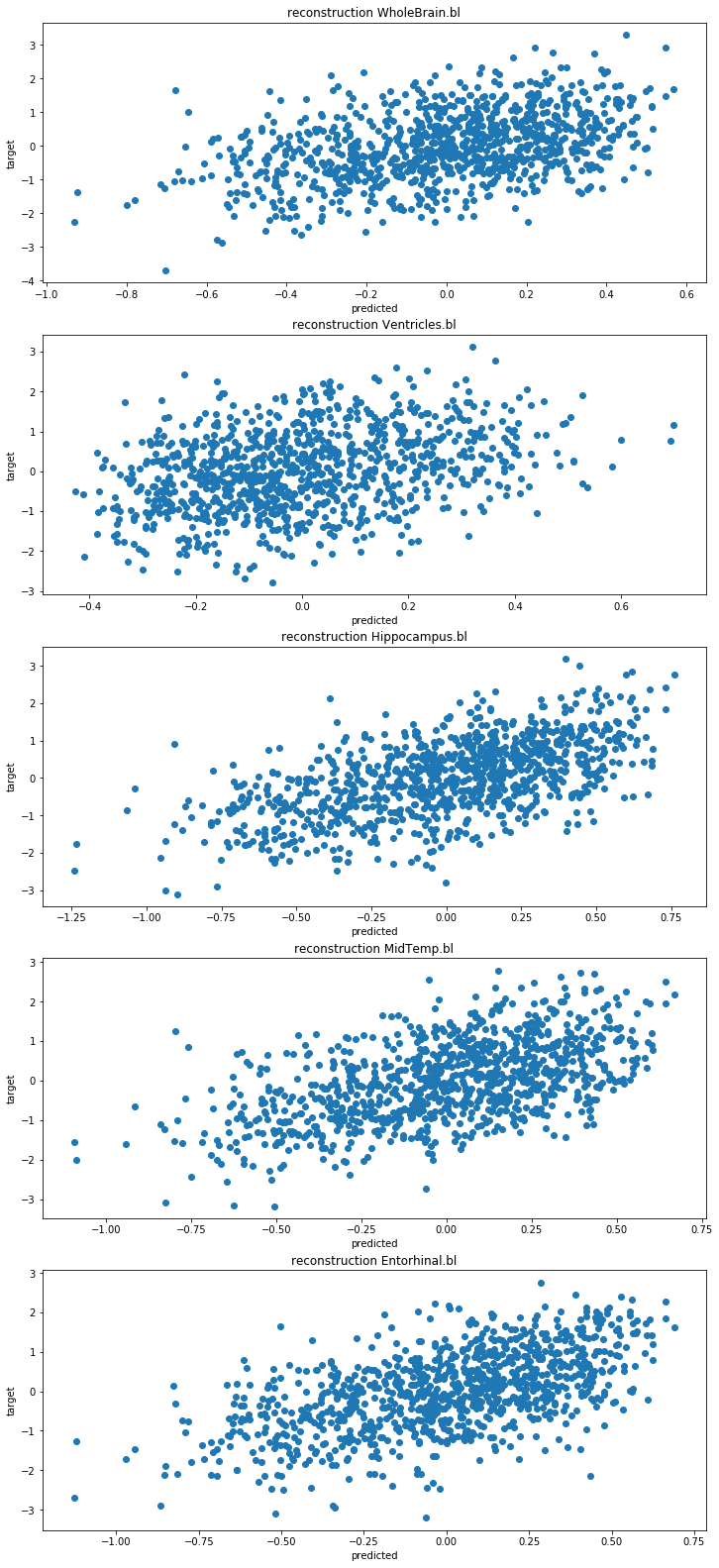
We are finally going to compare the multichannel model with the standard PLS modeling cognition and brain volumes jointly:
# FIT a PLS model to predict: cognition -> volume
plsca = PLSCanonical(n_components=1, scale = False)
plsca.fit(cognition_value, volumes_value)
PLSCanonical(n_components=1, scale=False)
# Compare (plot) the prediction of PLS against the true values and against the predictions of Mcvae.
# Are they correlated?
predicted_plsca = plsca.predict(cognition_value)
plt.figure(figsize=(26, 18))
for i in range(5):
plt.subplot(10,2,2*i+1)
plt.scatter(predicted_plsca[:,i], volumes_value[:,i])
plt.title('reconstruction' + volume_cols[i])
plt.xlabel('predicted')
plt.ylabel('target')
for i in range(5):
plt.subplot(10,2,2*i+2)
plt.scatter(predicted_plsca[:,i], decoding_volume_from_cognition[:,i])
plt.title('reconstruction' + volume_cols[i])
plt.xlabel('cca')
plt.ylabel('mcvae')
plt.show()
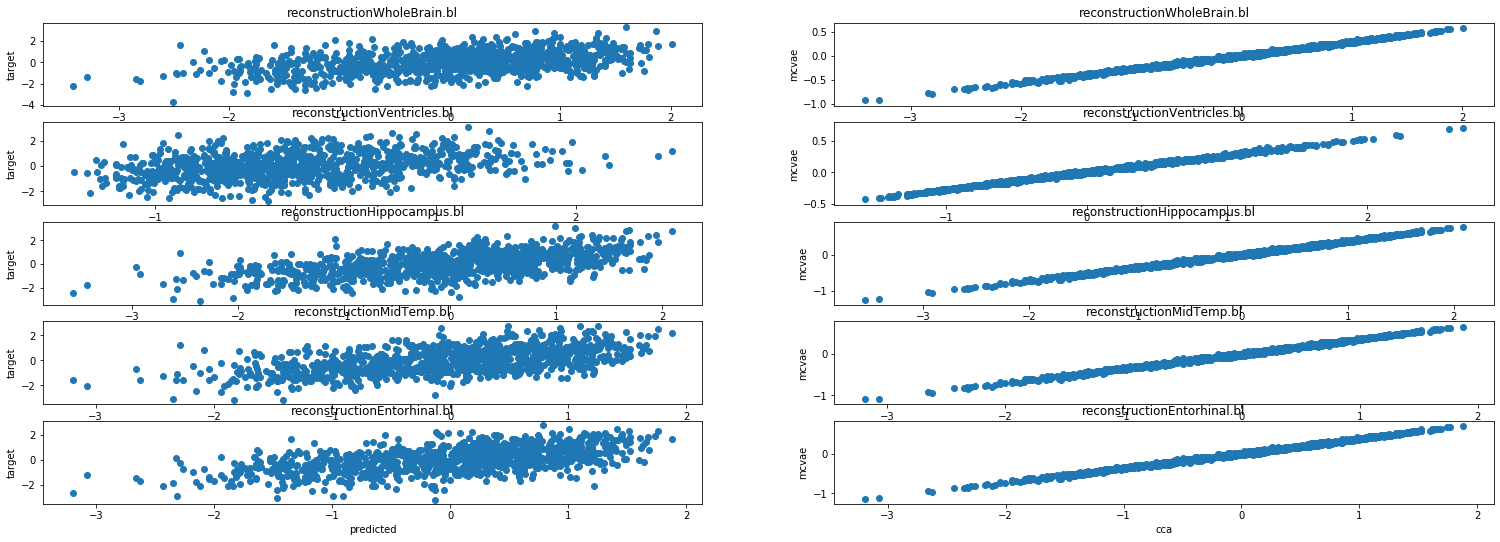
# Compare average reconstruction errors between PLS and Mcvae
print('Reconstruction error:')
print(f'PLS: {((predicted_plsca-volumes_value)**2).sum()}')
print(f'mcvae: {((decoding_volume_from_cognition-volumes_value)**2).sum()}')
Reconstruction error:
PLS: 4631.245631476227
mcvae: 3964.8306431191213
